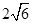题目内容

已知正方形ABCD的边长a，点E是AB的中点，在对角线BD上找一点P，且PE+PA的最小值为2根号5则a=      .
4
因为 点A关于直线BD的对称点是C，连接CE交BD于点P，
则CE=PE+PC=PE+PA=2根号5,
因E是AB的中点，所以BE=1/2AB=（1/2）a,
在直角三角形BEC中
BE2+BC2=EC2 
所以 (1/2 a,)2+a2=(2根号5)2 
则a=4
练习册系列答案
相关题目
如图，在平行四边形ABCD中，BD=2AB，AC与BD相交于点O，点E、F、G分别是OC、OB、AD的中点．
求证：（1）DE⊥OC；
（2）EG=EF．
如图，在Rt△ABC中，∠B=90°，AC=60，AB=30。点D是AC上的动点，过D作DF⊥BC于F，再过F作FE//AC，交AB于E。设CD=x，DF=y.
（1）求y与x的函数关系式；
（2）当四边形AEFD为菱形时，求x的值；
（3）当△FED是直角三角形时，求x的值.
如图，四边形ABCD的对角线AC、BD互相垂直，则下列条件能判定四边形ABCD为菱形的是
A.BA=BC         B.AB//CD     C.AC=BD        D.AC、BD互相平分
五边形的内角和是（  ）
A．180°B．360°C．540°D．600°
如图，已知等腰梯形ABCD的底角∠B=45°，高AE=1，上底AD=1，则其面积为   ．
如图，在△ABC中，AB＝AC＝10cm，BD⊥AC于D，且BD＝8cm．点M从点A出发，沿AC方向匀速运动，速度为2cm/s；同时直线PQ由点B出发沿BA方向匀速运动，速度为1cm/s，运动过程中始终保持PQ∥AC，直线PQ交AB于P，交BC于Q，连接PM，设运动时间为t（s）（0＜t＜5）．

（1）当四边形PQCM是平行四边形时，求t的值；
（2）当t为何值时，△PQM是等腰三角形？
（3）以PM为直径作⊙E，在点P、Q整个运动过程中，是否存在这样的时刻t，使得⊙E与BC相切？若存在，请求出运动时间t的值；若不存在，请说明理由．
如图，边长为1的菱形ABCD中，∠DAB=60度．连接对角线AC，以AC为边作第二个菱形ACC1D1，使∠D1AC=60°；连接AC1，再以AC1为边作第三个菱形AC1C2D2，使∠D2AC1=60°；…，按此规律所作的第n个菱形的边长为         ．
如图，在矩形ABCD中，AD＞AB，将矩形ABCD折叠，使点C与点A重合，折痕为MN，连结CN．若△CDN的面积与△CMN的面积比为1︰5，则 的值为（    ）.
A．2B．4C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网