题目内容
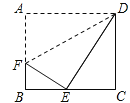
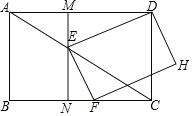
【题目】如图,在矩形ABCD中,AB=3,BC=4,点E是线段AC上的一个动点且![]() =k(0<k<1),点F在线段BC上,且DEFH为矩形;过点E作MN⊥BC,分别交AD,BC于点M,N.
=k(0<k<1),点F在线段BC上,且DEFH为矩形;过点E作MN⊥BC,分别交AD,BC于点M,N.
(1)求证:△MED∽△NFE;
(2)当EF=FC时,求k的值.
(3)当矩形EFHD的面积最小时,求k的值,并求出矩形EFHD面积的最小值.
【答案】(1)见解析;(2)![]() ;(3)矩形EFHD的面积最小值为
;(3)矩形EFHD的面积最小值为![]() ,k=
,k=![]() .
.
【解析】
(1)由矩形的性质得出∠B=90°,AD=BC=4,DC=AB=3,AD∥BC,证出∠EMD=∠FNE=90°,∠NEF=∠MDE,即可得出△MED∽△NFE;
(2)设AM=x,则MD=NC=4﹣x,由三角函数得出ME=![]() x,得出NE=3﹣
x,得出NE=3﹣![]() x,由相似三角形的性质得出
x,由相似三角形的性质得出![]() =
=![]() ,求出NF=
,求出NF=![]() x,得出FC=4﹣x﹣
x,得出FC=4﹣x﹣![]() x=4﹣
x=4﹣![]() x,由勾股定理得出EF=
x,由勾股定理得出EF=![]() =
=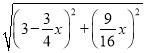 ,当EF=FC时,得出方程4﹣
,当EF=FC时,得出方程4﹣![]() x=
x=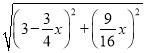 ,解得x=4(舍去),或x=
,解得x=4(舍去),或x=![]() ,进而得出答案;
,进而得出答案;
(3)由相似三角形的性质得出![]() =
=![]() =
=![]() ,得出DE=
,得出DE=![]() EF,求出矩形EFHD的面积=DE×EF=
EF,求出矩形EFHD的面积=DE×EF=![]() EF2=
EF2=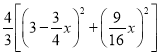 =
= ,由二次函数的性质进而得出答案.
,由二次函数的性质进而得出答案.
(1)证明:∵四边形ABCD是矩形,
∴∠B=90°,AD=BC=4,DC=AB=3,AD∥BC,
∵MN⊥BC,
∴MN⊥AD,
∴∠EMD=∠FNE=90°,
∵四边形DEFH是矩形,
∴∠MED+∠NEF=90°,
∴∠NEF=∠MDE,
∴△MED∽△NFE;
(2)解:设AM=x,则MD=NC=4﹣x,
∵tan∠DAC=tan∠MAE=![]() =
=![]() =
=![]() ,
,
∴ME=![]() x,
x,
∴NE=3﹣![]() x,
x,
∵△MED∽△NFE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:NF=![]() x,
x,
∴FC=4﹣x﹣![]() x=4﹣
x=4﹣![]() x,EF=
x,EF=![]() =
=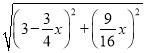 ,
,
当EF=FC时,4﹣![]() x=
x=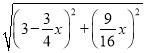 ,
,
解得:x=4或x=![]() ,
,
由题意可知x=4不合题意,
当x=![]() 时,AE=
时,AE=![]() ,
,
∵AC=![]() =
=![]() =5,
=5,
∴k=![]() =
=![]() ;
;
(3)解:由(1)可知:△MED∽△NFE,
∴![]() ,
,
∴DE=![]() EF,
EF,
∴矩形EFHD的面积=DE×EF=![]() EF2=
EF2=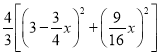 =
=
∴当![]() x﹣
x﹣![]() =0时,即x=
=0时,即x=![]() 时,矩形EFHD的面积最小,最小值为:
时,矩形EFHD的面积最小,最小值为:![]() ,
,
∵cos∠MAE=![]() =
=![]() =
=![]() ,
,
∴AE=![]() AM=
AM=![]() ×
×![]() =
=![]() ,
,
此时k=![]() =
=![]() .
.