��Ŀ����
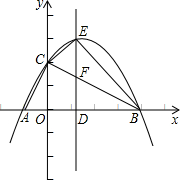 ��ͼƽ��ֱ������ϵ�У�������y=-
��ͼƽ��ֱ������ϵ�У�������y=-| 1 |
| 2 |
| 3 |
| 2 |
��1����֤����ABCΪֱ�������Σ�
��2��ֱ��x=m��0��m��4�����߶�OB���ƶ�����x���ڵ�D�����������ڵ�E����BC�ڵ�F����mΪ��ֵʱ��EF=DF��
��3������CE��BE�������⡰�Ƿ���������ĵ�E��ʹ��BCE��������С��ͬѧ��Ϊ������EΪ�����ߵĶ���ʱ����BCE�����������Ĺ۵��Ƿ���ȷ�������ļ��⣬����BCE������������ֵ���������E������͡�BCE����������
��������1���ȸ��������ߵĽ���ʽ���A��B��C��������꣬��ô�������ַ���������⣮
�ٿɷֱ����AC��BC��AB�ij���Ȼ���ù��ɶ�����֤��
�ڿɷֱ���ֱ��������AOC��BOC�У������Ǻ����ó���ص������ȣ�Ȼ��ͨ��֤Сֱ�����������BAC�������ó����ۣ�
��2��������������
�ٿɸ��ݡ�BDF�͡�BOC���ƣ���m��ʾ��DF�ij������ɵó�DE�ij���Ҳ�͵ó���E������꣬Ȼ��E��������������ߵĽ���ʽ�м��ɵó�m��ֵ��
�ڿ������ֱ��BC�Ľ���ʽ������DE=2DF����˵�x=mʱ�������ߵ�ֵ��ֱ��BC��ֵ��2�����ɴ˿ɵó�����m�ķ��̣��������m��ֵ��
��3������Ҫ�������BEC�������E������ĺ�����ϵʽ�����ݺ�������������⣮�����E������꣨������꣬�������ߵĽ���ʽ��ʾ�����꣩��Ȼ����ݡ�BCE�����=����CODE�����+��BDE�����-��BOC����������ó����ڡ�BCE�������E�������ĺ�����ϵʽ��Ȼ����ݺ������������S�����ֵ�Ͷ�Ӧ��E������꣮
�ٿɷֱ����AC��BC��AB�ij���Ȼ���ù��ɶ�����֤��
�ڿɷֱ���ֱ��������AOC��BOC�У������Ǻ����ó���ص������ȣ�Ȼ��ͨ��֤Сֱ�����������BAC�������ó����ۣ�
��2��������������
�ٿɸ��ݡ�BDF�͡�BOC���ƣ���m��ʾ��DF�ij������ɵó�DE�ij���Ҳ�͵ó���E������꣬Ȼ��E��������������ߵĽ���ʽ�м��ɵó�m��ֵ��
�ڿ������ֱ��BC�Ľ���ʽ������DE=2DF����˵�x=mʱ�������ߵ�ֵ��ֱ��BC��ֵ��2�����ɴ˿ɵó�����m�ķ��̣��������m��ֵ��
��3������Ҫ�������BEC�������E������ĺ�����ϵʽ�����ݺ�������������⣮�����E������꣨������꣬�������ߵĽ���ʽ��ʾ�����꣩��Ȼ����ݡ�BCE�����=����CODE�����+��BDE�����-��BOC����������ó����ڡ�BCE�������E�������ĺ�����ϵʽ��Ȼ����ݺ������������S�����ֵ�Ͷ�Ӧ��E������꣮
�����1��֤��������y=-
x2+
x+2
��y=0ʱ��-
x2+
x+2=0�����x1=-1��x2=4��
��x=0ʱ��y=2
��A��B��C���������ֱ�Ϊ
A��-1��0����B��4��0����C��0��2��
��OA=1��OB=4��OC=2��
��AB=OA+OB=5��
��AB2=25
��Rt��AOC��AC2=OA2+OC2=12+22=5
��Rt��COB��BC2=OC2+OB2=22+42=20
��AC2+BC2=AB2��
���ABC���ԡ�ACBΪֱ�ǵ�ֱ�������Σ�
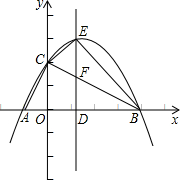
��2���⣺��ֱ��DE�Ľ���ʽΪֱ��x=m��
��OD=m��DE��OB��
��OC��AB��
��OC��DE��
���BDF�ס�BOC��
��
=
��OC=2��OB=4��BD=OB-OD=4-m��
��DF=
=
=2-
m��
��EF=DFʱ��DE=2DF=4-m��
��E���������m��4-m��
��E����������y=-
x2+
x+2�ϣ�
��4-m=-
m2+
m+2
���m1=1��m2=4��
��0��m��4��
��m=4��ȥ��
�൱m=1ʱ��EF=DF��
��3���⣺С��ͬѧ�Ĺ۵��Ǵ���ģ�
��OD=m��DE��OB��E����������y=-
x2+
x+2��
��E�������ɱ�ʾΪ��m��-
m2+
m+2��
��DE=-
m2+
m+2��
��DF=2-
m��
��EF=DE-DF=-
m2+2m
��S��BCE=S��CEF+S��BEF=
EF•OD+
EF•BD=
EF•��OD+BD��
=
EF•OB=
EF•4=2EF
��S��BCE=-m2+4m=-��m2-4m+4-4��=-��m-2��2+4
�൱m=2ʱ��S��BCE�����ֵ����BCE��������Ϊ4��
�ߵ�m=2ʱ��-
m2+
m+2=3��
��E���������2��3��
��������y=-
x2+
x+2�Ķ�������Ϊ��
��
����
��С��ͬѧ�Ĺ۵��Ǵ���ģ�
| 1 |
| 2 |
| 3 |
| 2 |
��y=0ʱ��-
| 1 |
| 2 |
| 3 |
| 2 |
��x=0ʱ��y=2
��A��B��C���������ֱ�Ϊ
A��-1��0����B��4��0����C��0��2��
��OA=1��OB=4��OC=2��
��AB=OA+OB=5��
��AB2=25
��Rt��AOC��AC2=OA2+OC2=12+22=5
��Rt��COB��BC2=OC2+OB2=22+42=20
��AC2+BC2=AB2��
���ABC���ԡ�ACBΪֱ�ǵ�ֱ�������Σ�
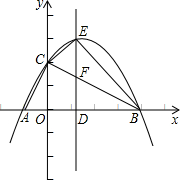
��2���⣺��ֱ��DE�Ľ���ʽΪֱ��x=m��
��OD=m��DE��OB��
��OC��AB��
��OC��DE��
���BDF�ס�BOC��
��
| DF |
| OC |
| BD |
| BO |
��OC=2��OB=4��BD=OB-OD=4-m��
��DF=
| BD•OC |
| BO |
| 2(4-m) |
| 4 |
| 1 |
| 2 |
��EF=DFʱ��DE=2DF=4-m��
��E���������m��4-m��
��E����������y=-
| 1 |
| 2 |
| 3 |
| 2 |
��4-m=-
| 1 |
| 2 |
| 3 |
| 2 |
���m1=1��m2=4��
��0��m��4��
��m=4��ȥ��
�൱m=1ʱ��EF=DF��
��3���⣺С��ͬѧ�Ĺ۵��Ǵ���ģ�
��OD=m��DE��OB��E����������y=-
| 1 |
| 2 |
| 3 |
| 2 |
��E�������ɱ�ʾΪ��m��-
| 1 |
| 2 |
| 3 |
| 2 |
��DE=-
| 1 |
| 2 |
| 3 |
| 2 |
��DF=2-
| 1 |
| 2 |
��EF=DE-DF=-
| 1 |
| 2 |
��S��BCE=S��CEF+S��BEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
��S��BCE=-m2+4m=-��m2-4m+4-4��=-��m-2��2+4
�൱m=2ʱ��S��BCE�����ֵ����BCE��������Ϊ4��
�ߵ�m=2ʱ��-
| 1 |
| 2 |
| 3 |
| 2 |
��E���������2��3��
��������y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
��С��ͬѧ�Ĺ۵��Ǵ���ģ�
������������Ҫ������κ�����Ӧ�á�ֱ�������ε��ж���ͼ�ε������֪ʶ���ۺ�Ӧ��֪ʶ����������������������ͼ�ε����ͨ��ת��Ϊ����ͼ�ε�����ĺͲ

��ϰ��ϵ�д�
�����Ŀ
 OA��OB��
OA��OB�� ����ͼƽ��ֱ������ϵ�У���ABC��������A��B��C������ֱ�ΪA��2��-1����B��1��-3����C��4��-4����
����ͼƽ��ֱ������ϵ�У���ABC��������A��B��C������ֱ�ΪA��2��-1����B��1��-3����C��4��-4���� ����ͼƽ��ֱ������ϵ�л�������y=-
����ͼƽ��ֱ������ϵ�л�������y=- 19����֪����ͼƽ��ֱ������ϵ�У���ABC������������ֱ�ΪA��-3��-2����B��-5��0����C��-2��4����
19����֪����ͼƽ��ֱ������ϵ�У���ABC������������ֱ�ΪA��-3��-2����B��-5��0����C��-2��4����