题目内容
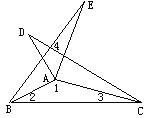
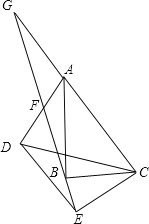
【题目】如图,在△ABC和△DEC中,∠ABC=∠DEC=90°,连接AD交射线EB于F,AC∥DE,延长CA交射线EB于点G,点F恰好是AD中点。
(1)求证:△AFG≌△DFE;
(2)若BC=CE,
①求证:∠ABF=∠DEF;
②若∠BAC=30°,试求∠AFG的度数。
【答案】(1)证明见解析(2)①证明见解析②∠AFG=60°。
【解析】试题分析:
(1)由AG∥DE易得:∠G=∠DEF;由F是AD的中点易得AF=DF,结合∠AFG=∠DFE,即可证得:△AGF≌△DEF;
(2)①由BC=CE可得∠CBE=∠CEB,结合∠ABC=DEC=90°,易得∠ABF+∠CBE=90°,∠CEB+∠DEF=90°,从而可得∠ABF=∠DEF;
②由△AGF≌△DEF可得∠G=∠DEF,AG=DE结合∠ABF=∠DEF,可得:∠ABF=∠G,从而可得:AG=AB,这样即可得到:AB=DE,结合∠ABC=∠DEC=90°,BC=CE即可证得:△ABC≌△DEC,由此可得AC=CD,∠EDC=∠BAC=30°,结合AC∥DE可得∠ACD=∠EDC=30°,从而可得∠CAD=![]() ;由∠BAC=∠G+∠ABG=30°结合∠G=∠ABG易得∠G=15°,结合∠CAD=∠G+∠AFG即可得到∠AFG=60°.
;由∠BAC=∠G+∠ABG=30°结合∠G=∠ABG易得∠G=15°,结合∠CAD=∠G+∠AFG即可得到∠AFG=60°.
试题解析:
(1)∵AG∥DE,点F是AD的中点,
∴∠G=∠DEF,AF=DF,
∵△AGF和△DEF中,
 ,
,
∴△AGF≌△DEF(AAS);
(2)① ∵BC=CE,
∴∠CBE=∠CEB,
∵∠ABC=DEC=90°,
∵∠ABF+∠CBE=90°,∠CEB+∠DEF=90°,
∴∠ABF=∠DEF;
②∵△AGF≌△DEF,
∴∠G=∠DEF,
∵∠ABF=∠DEF,
∴∠ABF=∠G,
∴AG=AB,
∵△AGF≌△DEF,
∴AG=DE,
∴DE=AB,
∵△ABC和△DEC中,
 ,
,
∴△ABC≌△DEC,(SAS)
∴AC=CD,∠BAC=∠EDC,
∵AC∥DE,
∴∠EDC=∠ACD,
∴∠ACD=∠BAC=30°,
∴∠CAD=75°,
∵∠ABF=∠G,∠BAC=30°,
∴∠G=15°,
∵∠CAD=∠G+∠AFG,
∴∠AFG=60°.