题目内容
【题目】已知代数式(mx2+2mx-1)(xm+3nx+2)化简以后是一个四次多项式,并且不含二次项,请分别求出m,n的值,并求出一次项系数.
【答案】m=2,n=-![]() ,一次项系数为
,一次项系数为![]() .
.
【解析】
先把代数式按照多项式乘以多项式展开,因为化简后是一个四次多项式,所以x的最高指数m+2=4;不含二次项,即二次项的系数为0,即可解答.
(mx2+2mx-1)(xm+3nx+2)=mxm+2+3mnx3+2mx2+2mxm+1+6mnx2+4mx-xm-3nx-2,
因为该多项式是四次多项式,
所以m+2=4,解得m=2.
所以原式=2x4+(6n+4)x3+(3+12n)x2+(8-3n)x-2.
因为多项式不含二次项,
所以3+12n=0,解得n=-![]() ,
,
所以一次项系数为8-3n=![]() .
.

练习册系列答案
相关题目
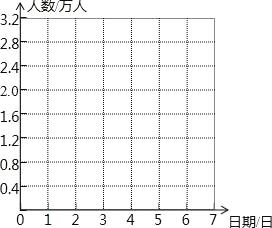
【题目】“十一”黄金周期间,深圳世界之窗风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 单位:万人 | +1.6 | +0.8 | +0.4 | ﹣0.4 | ﹣0.8 | +0.2 | ﹣1.2 |
(1)请判断七天内游客人数最多的是 日,最少的是 日.
(2)以9月30日的游客人数为0点,用折线统计图表示这7天的游客人数的变化情况.