Question

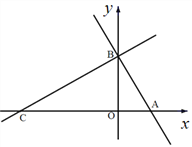
【题目】如图，在平面直角坐标系中，点为坐标原点．已知：抛物线经过点和点．

（）试判断该抛物线与轴交点的情况．

（）平移这条抛物线，使平移后的抛物线经过点，且与轴交于点，同时满足以， ， 为顶点的三角形是等腰直角三角形．请你写出平移过程，并说明理由．

Answer 1

【答案】（1）抛物线与轴有两个交点；（2）将原抛物线向右平移个单位，再向下平移个单位即可．

【解析】试题分析：（1）把P、Q两点的坐标代入抛物线解析式可求得a、b的值，可求得抛物线解析式，再根据一元二次方程根的判别式，可判断抛物线与x轴的交点情况；

（2）利用A点坐标和等腰三角形的性质可求得B点坐标，设出平移后的抛物线的解析式，把A、B的坐标代入可求得平移后的抛物线的解析式，比较平移前后抛物线的顶点的变化即可得到平移的过程．

解：（）将， 代入中得

．

解得： ．

∴抛物线为．

．

．

．

∴抛物线与轴有两个交点．

一个交在轴正半轴，一个交在轴负半轴，且正半轴交点离原点更远．

（）∵是等腰直角三角形， ，点在轴上，

∴点坐标为或．

可设平移后的抛物线解析式为．

①当抛物线过点， 时，代入可得．

，解得．

∴平移后的抛物线为．

∴该抛物线的顶点坐标为，而原抛物线顶点坐标为．

∴将原抛物线向右平移个单位，再向上平移个单位即可．

②当抛物线过点， 时，代入可得．

，解得．

∴平移后的抛物线为．

∴该抛物线的顶点坐标为，而原抛物线顶点坐标为．

∴将原抛物线向右平移个单位，再向下平移个单位即可．