题目内容
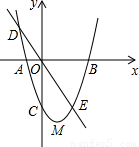
如图,已知二次函数y=ax2+bx-3的图象经过二点A(-1,0),B(3,0),它的顶点为M,且正比例函数y=kx的图象与二次函数的图象相交于D、E两点.(1)求该二次函数的解析式和顶点M的坐标;
(2)若点E的坐标是(2.-3),且二次函数的值大于正比例函数的值时,试根据函数图象求出符合条件的自变量x的取值范围;
(3)将二次函数图象沿x轴向右平移2个单位长度,求所得图象对应的函数关系式.
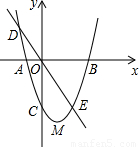
【答案】分析:(1)设二次函数的解析式为y=a(x+1)(x-3),把(0,-3)代入即可求出a的值,即得到二次函数的解析式,把它化成顶点式即可求出顶点坐标;
(2)把E(2,-3)代入y=kx即可求出正比例函数的解析式,解由二次函数的解析式和正比例函数的解析式组成的方程组即可求出交点D的坐标,根据图象即可求出符合条件的自变量x的取值范围;
(3)由(1)中的二次函数解析式,根据函数平移的规律解答即可.
解答:解:(1)设二次函数的解析式为y=a(x+1)(x-3),
把(0,-3)代入得:a=1,
则二次函数的解析式为y=(x+1)(x-3),
即:y=x2-2x-3,
配方得:y=(x-1)2-4,
则顶点M的坐标是(1,-4).
答:该二次函数的解析式是y=x2-2x-3,顶点M的坐标是(1,-4).
(2)把E(2,-3)代入y=kx得:k=- ,
,
则正比例函数的解析式为y=- x,
x,
∵把正比例函数与二次函数的解析式组成方程组
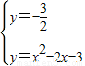 ,
,
解得: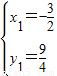 ,
,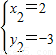 ,
,
∴D(- ,
, ),E(2,-3),
),E(2,-3),
∴当二次函数的值大于正比例函数的值时,由图可知:x>2或x<- ;
;
(3)∵y=(x-1)2-4,
∴二次函数图象沿x轴向右平移2个单位长度时:y=(x-1-2)2-4,
即y=x2-6x+5.
点评:本题主要考查了用待定系数法求一次函数、二次函数的解析式,解二元二次方程组,求一次函数、二次函数的解析式和交点坐标是解此题的关键,此题题型较好,综合性比较强.
(2)把E(2,-3)代入y=kx即可求出正比例函数的解析式,解由二次函数的解析式和正比例函数的解析式组成的方程组即可求出交点D的坐标,根据图象即可求出符合条件的自变量x的取值范围;
(3)由(1)中的二次函数解析式,根据函数平移的规律解答即可.
解答:解:(1)设二次函数的解析式为y=a(x+1)(x-3),
把(0,-3)代入得:a=1,
则二次函数的解析式为y=(x+1)(x-3),
即:y=x2-2x-3,
配方得:y=(x-1)2-4,
则顶点M的坐标是(1,-4).
答:该二次函数的解析式是y=x2-2x-3,顶点M的坐标是(1,-4).
(2)把E(2,-3)代入y=kx得:k=-
 ,
,则正比例函数的解析式为y=-
 x,
x,∵把正比例函数与二次函数的解析式组成方程组
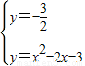 ,
,
解得:
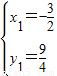 ,
,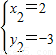 ,
,∴D(-
 ,
, ),E(2,-3),
),E(2,-3),∴当二次函数的值大于正比例函数的值时,由图可知:x>2或x<-
 ;
;(3)∵y=(x-1)2-4,
∴二次函数图象沿x轴向右平移2个单位长度时:y=(x-1-2)2-4,
即y=x2-6x+5.
点评:本题主要考查了用待定系数法求一次函数、二次函数的解析式,解二元二次方程组,求一次函数、二次函数的解析式和交点坐标是解此题的关键,此题题型较好,综合性比较强.

练习册系列答案
相关题目
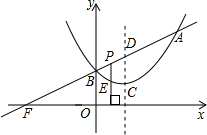 三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
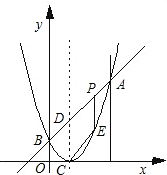 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.
如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.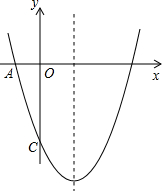 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).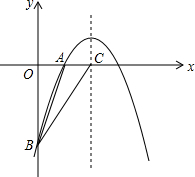 (2012•衡水一模)如图,已知二次函数
(2012•衡水一模)如图,已知二次函数