题目内容
【题目】解不等式组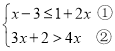
请结合题意填空，完成本题的解答.
（Ⅰ）解不等式①，得___________；
（Ⅱ）解不等式②，得___________；
（Ⅲ）把不等式①和②的解集在数轴上表示出来：
（Ⅳ）原不等式组的解集为___________.
【答案】（Ⅰ）x
（Ⅱ）
（Ⅲ）见解析（Ⅳ）
【解析】
Ⅰ.先移项合并，再未知数的系数化为1，即可得到不等式的解集
Ⅱ.先移项合并，再未知数的系数化为1即可得到不等式的解集
Ⅲ.根据求出每一个不等式的解集，将解集表示在数轴上表示出来；
Ⅳ.根据在数轴上表示出来不等式的解集，从而确定不等式组的解集．
解：Ⅰ.解不等式①，得
. ∴x；
故答案为：x
Ⅱ.解不等式②，得.
故答案为：
Ⅲ. 把不等式①和②的解集在数轴上表示出来．如图：
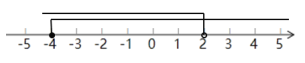
Ⅳ.原不等式组的解集为.
故答案为：.
练习册系列答案
相关题目
【题目】某公司要购买一种笔记本供员工学习时使用.在甲文具店不管一次购买多少本，每本价格为2元.在乙文具店购买同样的笔记本，一次购买数量不超过20时，每本价格为2.4元；一次购买数量超过20时，超过部分每本价格为1.8元.
设在同一家文具店一次购买这种笔记本的数量为x(x为非负整数).
(Ⅰ)根据题意，填写下表：
一次购买数量(本) | 10 | 20 | 30 | 40 | … |
甲文具店付款金额(元) | 20 | 60 | … | ||
乙文具店付款金额(元) | 24 | 66 | … |
(Ⅱ)设在甲文具店购买这种笔记本的付款金额为
元，在乙文具店购买这种笔记本的付款金额为
元，分别写出，关于
的函数关系式；
(Ⅲ)当
时，在哪家文具店购买这种笔记本的花费少？请说明理由.
