题目内容
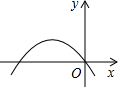 如图所示的抛物线是二次函数y=ax2-3x+a2-1的图象,那么下列结论错误的是
如图所示的抛物线是二次函数y=ax2-3x+a2-1的图象,那么下列结论错误的是
- A.当y<0时,x>0
- B.当-3<x<0时,y>0
- C.当x<
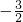 时,y随x的增大而增大
时,y随x的增大而增大 - D.上述抛物线可由抛物线y=-x2平移得到
A
分析:由图象可知,抛物线经过原点(0,0),二次函数y=ax2-3x+a2-1与y轴交点纵坐标为a2-1,所以a2-1=0,解得a的值.再图象开口向下,a<0确定a的值,进而得出二次函数的解析式,即可得出答案.
解答:由图象可知,抛物线经过原点(0,0),
所以a2-1=0,解得a=±1,
∵图象开口向下,a<0,
∴a=-1.
∴y=-x2-3x,
∴二次函数与图象的交点为:(-3,0),(0,0),
∴当y<0时,x<-3或x>0,故A选项错误;
当-3<x<0时,y>0,故B选项正确;
当x<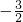 时,y随x的增大而增大故C选项正确;
时,y随x的增大而增大故C选项正确;
上述抛物线可由抛物线y=-x2平移得到,故D选项正确;
故选:A.
点评:此题主要考查了二次函数图象点的性质,从图象上把握有用的条件,准确选择数量关系解得a的值,简单的图象最少能反映出2个条件:开口向下a<0;经过原点a2-1=0,利用这两个条件即可求出a的值进而得出二次函数的解析式是解题关键.
分析:由图象可知,抛物线经过原点(0,0),二次函数y=ax2-3x+a2-1与y轴交点纵坐标为a2-1,所以a2-1=0,解得a的值.再图象开口向下,a<0确定a的值,进而得出二次函数的解析式,即可得出答案.
解答:由图象可知,抛物线经过原点(0,0),
所以a2-1=0,解得a=±1,
∵图象开口向下,a<0,
∴a=-1.
∴y=-x2-3x,
∴二次函数与图象的交点为:(-3,0),(0,0),
∴当y<0时,x<-3或x>0,故A选项错误;
当-3<x<0时,y>0,故B选项正确;
当x<
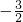 时,y随x的增大而增大故C选项正确;
时,y随x的增大而增大故C选项正确;上述抛物线可由抛物线y=-x2平移得到,故D选项正确;
故选:A.
点评:此题主要考查了二次函数图象点的性质,从图象上把握有用的条件,准确选择数量关系解得a的值,简单的图象最少能反映出2个条件:开口向下a<0;经过原点a2-1=0,利用这两个条件即可求出a的值进而得出二次函数的解析式是解题关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
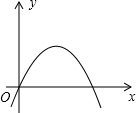 如图所示的抛物线是二次函数y=ax2+5x+4-a2的图象,那么a的值是( )
如图所示的抛物线是二次函数y=ax2+5x+4-a2的图象,那么a的值是( )| A、2 | ||
| B、-2 | ||
C、-
| ||
| D、±2 |

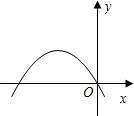 14、如图所示的抛物线是二次函数y=-x2+ax+a2-4的图象,那么a的值是
14、如图所示的抛物线是二次函数y=-x2+ax+a2-4的图象,那么a的值是 如图所示的抛物线是二次函数y=ax2+x+a2-1的图象,那么a的值是
如图所示的抛物线是二次函数y=ax2+x+a2-1的图象,那么a的值是 如图所示的抛物线是二次函数y=(m-2)x2-3x+m2+m-6的图象,那么m的值是
如图所示的抛物线是二次函数y=(m-2)x2-3x+m2+m-6的图象,那么m的值是