题目内容
如图所示的抛物线是二次函数y=（m-2）x2-3x+m2+m-6的图象，那么m的值是-3
-3
．分析：由图可知，二次函数图象经过坐标原点，然后代入函数解析式进行计算即可求出m的值，再根据抛物线开口向下求出m的取值范围，从而得解．
解答：解：∵二次函数y=（m-2）x2-3x+m2+m-6经过（0，0），
∴m2+m-6=0，
解得m1=2，m2=-3，
∵抛物线开口向下，
∴m-2＜0，
解得m＜2，
∴m=-3．
故答案为：-3．
∴m2+m-6=0，
解得m1=2，m2=-3，
∵抛物线开口向下，
∴m-2＜0，
解得m＜2，
∴m=-3．
故答案为：-3．
点评：本题考查了二次函数图象，观察图形得到抛物线经过坐标原点是解题的关键，要注意根据抛物线的开口方向确定出m的取值范围，这也是本题容易出错的地方．
练习册系列答案
相关题目
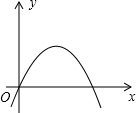如图所示的抛物线是二次函数y=ax2+5x+4-a2的图象，那么a的值是（ ）| A、2 | ||
| B、-2 | ||
C、-
| ||
| D、±2 |
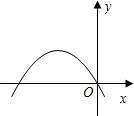14、如图所示的抛物线是二次函数y=-x2+ax+a2-4的图象，那么a的值是
如图所示的抛物线是二次函数y=ax2+x+a2-1的图象，那么a的值是