题目内容
【题目】在平面直角坐标系中,![]() 的顶点坐标分别为
的顶点坐标分别为![]() ,
,![]() ,
,![]() .
.
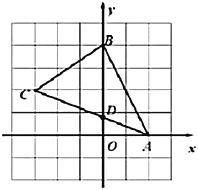
(1)求![]() 的面积.
的面积.
(2)若![]() 交
交![]() 轴于点
轴于点![]() ,请求出
,请求出![]() 点的坐标.
点的坐标.
【答案】(1)8;(2)(0,0.8)
【解析】
(1)用一个长方形将△ABC框住,再用长方形的面积减去三个直角三角形的面积即可;
(2)根据S△DBC+S△ABD =S△ABC,即可求出BD的长,从而求出D点坐标.
解:(1)用一个长方形将△ABC框住,如下图所示,
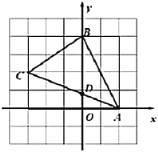
∴S△ABC=5×4-![]() ×3×2-
×3×2-![]() ×2×5-
×2×5-![]() ×2×4=8;
×2×4=8;
(2)设过C点平行于x轴的网格线交y轴于点E
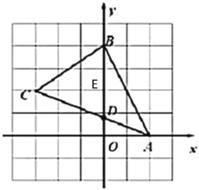
∵![]() ,
,![]()
![]()
∴AO=2,OB=4,CE=3
∵S△DBC+S△ABD =S△ABC
即![]() BD·CE+
BD·CE+![]() BD·AO=8
BD·AO=8
∴![]() BD·3+
BD·3+![]() BD·2=8
BD·2=8
解得:![]()
∵OD= OB-BD=0.8
即D点坐标为(0,0.8).

【题目】一次中学生田径运动会上,参加男子跳高的20名运动员成绩如下所示:
成绩(单位:米) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 | 1.85 | 1.90 |
人数 | 2 | 3 | 2 | 4 | 5 | 2 | 1 | 1 |
则下列叙述正确的是( )
A. 这些运动员成绩的中位数是1.70
B. 这些运动员成绩的众数是5
C. 这些运动员的平均成绩是1.71875
D. 这些运动员成绩的中位数是1.726
【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
A型 | B型 | |
进价(元/盏) | 40 | 65 |
售价(元/盏) | 60 | 100 |
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?
(3)若该商场预计用不少于2500元且不多于2600元的资金购进这批台灯,为了打开B种台灯的销路,商场决定每售出一盏B种台灯,返还顾客现金a元(10<a<20),问该商场该如何进货,才能获得最大的利润?