题目内容
 如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论:(1)点E和点F,B和D是关于中心O的对称点;(2)直线BD必经过点O;(3)四边形ABCD是中心对称图形;(4)四边形DEOC与四边形BFOA的面积必相等;(5)△AOE与△COF成中心对称,其中正确的个数为
如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论:(1)点E和点F,B和D是关于中心O的对称点;(2)直线BD必经过点O;(3)四边形ABCD是中心对称图形;(4)四边形DEOC与四边形BFOA的面积必相等;(5)△AOE与△COF成中心对称,其中正确的个数为
- A.1个
- B.2个
- C.3个
- D.5个
D
分析:由于△ABC与△CDA关于点O对称,那么可得到AB=CD、AD=BC,即四边形ABCD是平行四边形,由于平行四边形是中心对称图形,且对称中心是对角线交点,可根据上述特点对各结论进行判断.
解答:△ABC与△CDA关于点O对称,则AB=CD、AD=BC,所以四边形ABCD是平行四边形,
因此点O就是?ABCD的对称中心,则有:
(1)点E和点F;B和D是关于中心O的对称点,正确;
(2)直线BD必经过点O,正确;
(3)四边形ABCD是中心对称图形,正确;
(4)四边形DEOC与四边形BFOA的面积必相等,正确;
(5)△AOE与△COF成中心对称,正确;
其中正确的个数为5个,故选D.
点评:熟练掌握平行四边形的性质和中心对称图形的性质是解决此题的关键.
分析:由于△ABC与△CDA关于点O对称,那么可得到AB=CD、AD=BC,即四边形ABCD是平行四边形,由于平行四边形是中心对称图形,且对称中心是对角线交点,可根据上述特点对各结论进行判断.
解答:△ABC与△CDA关于点O对称,则AB=CD、AD=BC,所以四边形ABCD是平行四边形,
因此点O就是?ABCD的对称中心,则有:
(1)点E和点F;B和D是关于中心O的对称点,正确;
(2)直线BD必经过点O,正确;
(3)四边形ABCD是中心对称图形,正确;
(4)四边形DEOC与四边形BFOA的面积必相等,正确;
(5)△AOE与△COF成中心对称,正确;
其中正确的个数为5个,故选D.
点评:熟练掌握平行四边形的性质和中心对称图形的性质是解决此题的关键.

练习册系列答案
相关题目
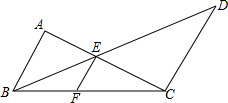 如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.
如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.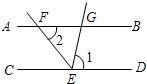 5、如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为( )
5、如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为( )
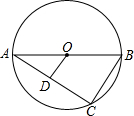 如图所示,已知AB为圆O的直径,AC为弦,OD∥BC交AC于D,OD=2cm,求BC的长.
如图所示,已知AB为圆O的直径,AC为弦,OD∥BC交AC于D,OD=2cm,求BC的长.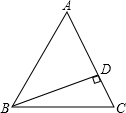 如图所示,已知AB=AC,BD⊥AC,试说明∠BAC=2∠CBD.
如图所示,已知AB=AC,BD⊥AC,试说明∠BAC=2∠CBD.