Question

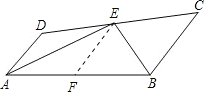
【题目】如图：E在线段CD上，EA、EB分别平分∠DAB和∠CBA，∠AEB=90°，设AD=，BC=，且．

（1）求AD和BC的长；

（2）你认为AD和BC还有什么关系？并验证你的结论；

（3）取AB中点F，连接EF,且EF∥AD∥BC。若EF=，你能求出AB的长度吗？若能，请写出推理过程；若不能，请说明理由．

Answer 1

【答案】（1）AD=3，BC=4；（2）AD∥BC，理由见解析；（3）能．7．

【解析】分析：（1）根据题意可知x-3=0，y-4=0，易求解AD和BC的长；（2）根据∠AEB=90°，可得∠EAB+∠EBA=90°，因为EA、EB分别平分∠DAB和∠CBA，则∠DAB+∠ABC=180°，所以AD∥BC；（3）如图，过E作EF∥AD，交AB于F，则∠DAE=∠AEF，∠EBC=∠BEF，因为EA、EB分别平分∠DAB和∠CBA，所以AF=EF=FB，再根据梯形中位线定理易求AB的长．

详解：（1）∵AD=x，BC=y，且（x﹣3）2+|y﹣4|=0，∴AD=3，BC=4．

（2）AD∥BC，

理由是：∵在△AEB中，∠AEB=90°，∴∠EAB+∠EBA=90°，

又∵EA、EB分别平分∠DAB和∠CBA，∴∠DAB+∠ABC=180°．

∴AD∥BC．

（3）能．

如图，

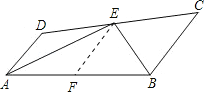
∵AD∥EF∥BC，则∠DAE=∠AEF，∠EBC=∠BEF，

∵EA、EB分别平分∠DAB和∠CBA，

∴∠EAF=∠AEF，∠EBF=∠BEF，

∴AF=EF=FB，又∵EF=，

∴AB=7．