题目内容
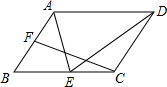 已知F是平行四边形ABCD中AB的中点,E是BC边上任意一点,若S△ACF=2,则S△AED=
已知F是平行四边形ABCD中AB的中点,E是BC边上任意一点,若S△ACF=2,则S△AED=分析:S△ACF=
S△ACB=
S?ABCD,又∵S△ADE=
S?ABCD,继而即可求出S△AED的值.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
解答:解:根据三角形和平行四边形的面积公式可知:S△ACF=
S△ACB=
S?ABCD,
又∵S△ADE=
S?ABCD,S△ACF=2,
∴S△ADE=2S△ACF=4.
故答案为:4.
| 1 |
| 2 |
| 1 |
| 4 |
又∵S△ADE=
| 1 |
| 2 |
∴S△ADE=2S△ACF=4.
故答案为:4.
点评:本题主要考查平行四边形的性质及简单的面积计算问题,难度适中,解题关键是准确找出各个图形之间的面积关系.

练习册系列答案
相关题目
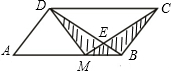 如图,已知M是平行四边形ABCD中AB边的三等分点,BD与CM交于E,则阴影部分面积与平行四边形面积比为( )
如图,已知M是平行四边形ABCD中AB边的三等分点,BD与CM交于E,则阴影部分面积与平行四边形面积比为( )| A、1:3 | B、1:4 | C、5:12 | D、7:24 |
 22、如图,已知E是平行四边形ABCD的边BC上的一点,F是BC延长线上一点,且BE=CF,BD与AE相交于点G.
22、如图,已知E是平行四边形ABCD的边BC上的一点,F是BC延长线上一点,且BE=CF,BD与AE相交于点G.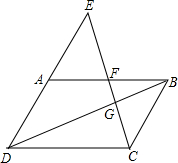 于点F、G.
于点F、G.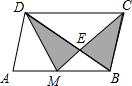 如图所示,已知M是平行四边形ABCD的AB边的中点,CM交BD于点E,BD=3BE,则图中阴影部分面积与平行四边形ABCD面积之比为
如图所示,已知M是平行四边形ABCD的AB边的中点,CM交BD于点E,BD=3BE,则图中阴影部分面积与平行四边形ABCD面积之比为