题目内容
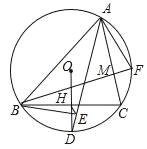
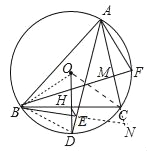
【题目】如图,△ABC内接于⊙O,D是弧BC的中点,OD交BC于点H,且OH=DH,连接AD,过点B作BE⊥AD于点E,连接EH,BF⊥AC于M,若AC=5,EH=![]() ,则AF=_____.
,则AF=_____.
【答案】![]()
【解析】如图,延长BE交AC的延长线于N,连接OB、OC、BD.
∵![]() ,
,
∴∠EAB=∠EAN,
∵AD⊥BN,
∴∠AEB=∠AEN=90°,
∴∠ABE+∠BAE=90°,∠N+∠EAN=90°,
∴∠ABE=∠N,
∴AB=AN,
∴BE=EN,
∵OD⊥BC,
∴BH=HC,
∴CN=2EH,
∴AB=AN=AC+CN=8,
∵OH=HD,BH⊥OD,
∴BO=BD=OD,
∴∠BOD=∠DOC=60°,
∴∠BAC=![]() ∠BOC=60°,
∠BOC=60°,
在Rt△AMB中,AM=![]() AB=4,BM=4
AB=4,BM=4![]() ,
,
在Rt△BMC中,BC=![]() ,
,
∵∠MAF=∠MBC,∠AMF=∠BMC,
∴△AMF∽△BMC,
∴![]() ,
,
∴![]() ,
,
∴AF=![]() .
.
故答案为![]() .
.

练习册系列答案
相关题目