��Ŀ����
����Ŀ����ͼ����֪�����ϵ�![]() ��ʾ����Ϊ10��
��ʾ����Ϊ10��![]() ��������λ�ڵ�
��������λ�ڵ�![]() ���һ�㣬��
���һ�㣬��![]() ������
������![]() �ӵ�
�ӵ�![]() ��������ÿ��5����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊ
��������ÿ��5����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊ![]() ��.
��.
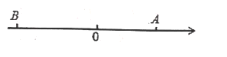
��1�������ϵĵ�![]() ��ʾ������___________����
��ʾ������___________����![]() ��ʾ������__________���ú�
��ʾ������__________���ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2����![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬
���е㣬![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬�ڵ�
���е㣬�ڵ�![]() �˶��Ĺ����У��߶�
�˶��Ĺ����У��߶�![]() �ij�����__________��
�ij�����__________��
��3������![]() �ӵ�
�ӵ�![]() ����������ÿ��3����λ���ȵ��ٶ����������������˶�������
����������ÿ��3����λ���ȵ��ٶ����������������˶�������![]() ͬʱ�������ʵ�
ͬʱ�������ʵ�![]() �˶�������ʱ���
�˶�������ʱ���![]() ���4����λ���ȣ�
���4����λ���ȣ�
���𰸡���1����-20��10-5t����2��15����3��13��17�룮
��������
��1������������빫ʽ���B���ʾ����������P���A���ʾ����С5t���P�㣻
��2�������е㹫ʽ���M��N�����ʾ�������ٸ���������빫ʽ���MN���ɣ�
��3������P����Q����ߺ�P����Q���ұ߷ֱ��з��̽�ɣ�
�⣺��1���ߵ�A��ʾ����Ϊ10��B��A����ߣ�AB=30��
�������ϵ�B��ʾ����Ϊ10-30=-20��
�߶���P�ӵ�A��������ÿ��5����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룬
���P��ʾ����Ϊ10-5t��
�ʴ�Ϊ��-20��10-5t��
��2���߶�MN�ij��Ȳ������仯��������15���������£�
�ٵ���P�ڵ�A��B����֮���˶�ʱ��![]()
��MΪ�߶�AP���е㣬NΪ�߶�BP���е㣬
��MN=MP+NP=![]() AP+
AP+![]() BP=
BP=![]() ��AP+BP��=
��AP+BP��=![]() AB=15��
AB=15��
�ڵ���P�˶�����B�����ʱ��![]()
��MΪ�߶�AP���е㣬NΪ�߶�BP���е㣬
��MN=MP-NP=![]() AP-
AP-![]() BP=
BP=![]() ��AP-BP��=
��AP-BP��=![]() AB=15��
AB=15��
�������������߶�MN�ij��Ȳ������仯����ֵΪ15��
��3������P��Qͬʱ���������P�˶�t��ʱ���Q����Ϊ4����λ���ȣ�
�ٵ�P��Q����֮ǰ��
�������4+5t=30+3t�����t=13��
�ڵ�P��Q����֮��
�������5t-4=30+3t�����t=17��
������P��Qͬʱ������13��17��ʱP��Q֮��ľ���ǡ�õ���4��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�