题目内容
Rt△ABC中,∠C=90°,CD为斜边AB上的高,若BC=4,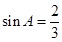 ,则BD的长为 。
,则BD的长为 。
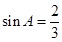 ,则BD的长为 。
,则BD的长为 。 .
.试题分析:因为CD为斜边AB上的高,所以∠BCD=∠A,根据
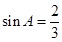 可求出BD的长.
可求出BD的长.试题解析:∵CD⊥AB
∴∠BCD+∠B=90°,
又∠A+∠B=90°,
∴∠BCD=∠A,
∴
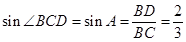 ,
,∴BD=
 .
.考点: 锐角三角函数.

练习册系列答案
相关题目
题目内容
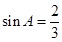 ,则BD的长为 。
,则BD的长为 。 .
.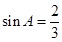 可求出BD的长.
可求出BD的长.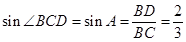 ,
, .
.