题目内容
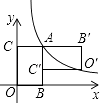
【题目】如图,已知双曲线 ![]() (x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE=
(x>0)经过矩形OABC的边AB、BC上的点F、E,其中CE= ![]() CB,AF=
CB,AF= ![]() AB,且四边形OEBF的面积为2,则k的值为 .
AB,且四边形OEBF的面积为2,则k的值为 . 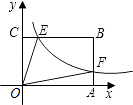
【答案】1
【解析】解:设矩形的长为a,宽为b,
则由CE= ![]() CB,AF=
CB,AF= ![]() AB,得:
AB,得:
CE= ![]() a,AF=
a,AF= ![]() b,
b,
∴三角形COE的面积为: ![]() ab,
ab,
三角形AOF的面积为: ![]() ab,
ab,
矩形的面积为:ab,
四边形OEBF的面积为:ab﹣ ![]() ab﹣
ab﹣ ![]() ab=
ab= ![]() ab,
ab,
∴ ![]() =
= ![]() ,
,
∴三角形AOF的面积=四边形OEBF的面积× ![]() =2×
=2× ![]() =
= ![]() ,
,
∴ ![]() |k|=
|k|= ![]() ,
,
又由于反比例函数的图象位于第一象限,k>0;
∴k=1.
所以答案是:1.
【考点精析】解答此题的关键在于理解比例系数k的几何意义的相关知识,掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积,以及对三角形的面积的理解,了解三角形的面积=1/2×底×高.

练习册系列答案
相关题目
【题目】某服装店用6000元购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价﹣进价),这两种服装的进价、标价如下表所示:
类型 价格 | A型 | B型 |
进价(元/件) | 60 | 100 |
标价(元/件) | 100 | 160 |
(1)求这两种服装各购进的件数;
(2)如果A中服装按标价的8折出售,B中服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价售出少收入多少元?