题目内容
 如图,⊙O是等边三角形ABC的外接圆,已知△ABC的边长为a,求图中阴影部分的面积.
如图,⊙O是等边三角形ABC的外接圆,已知△ABC的边长为a,求图中阴影部分的面积.
分析:圆的面积减去三角形的面积就得到阴影部分的面积.
解答: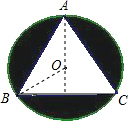 解:连接AO并延长与BC交于D,连接BO.(1分)
解:连接AO并延长与BC交于D,连接BO.(1分)
∵△ABC是等腰三角形,
∴AD⊥BC,且BD=DC,
∴AD平分∠BAC.
同理BO平分∠ABC,(2分)
∴AD=AB×sin60°=
a,(3分)
BO=
=
=
a,(4分)
∴S△ABC=
AD×BC=
×
a•a=
a2,(5分)
S⊙o=π•BO2=
a2π,(6分)
∴阴影部分的面积为:S=S⊙o-S△ABC=
a2π-
a2.(8分)
 解:连接AO并延长与BC交于D,连接BO.(1分)
解:连接AO并延长与BC交于D,连接BO.(1分)∵△ABC是等腰三角形,
∴AD⊥BC,且BD=DC,
∴AD平分∠BAC.
同理BO平分∠ABC,(2分)
∴AD=AB×sin60°=
| ||
| 2 |
BO=
| BD |
| cos∠OBD |
| a |
| 2•cos30° |
| 1 | ||
|
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
S⊙o=π•BO2=
| 1 |
| 3 |
∴阴影部分的面积为:S=S⊙o-S△ABC=
| 1 |
| 3 |
| ||
| 4 |
点评:正多边形的计算一般要经过中心作边的垂线,并连接中心与一个端点构造直角三角形,把正多边形的计算转化为解直角三角形.

练习册系列答案
相关题目
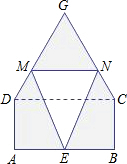 某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆. 26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.
26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形. 下滑动且始终保持和AB平行的伸缩横杆,△EMN是随MN滑动而变化的三角通风窗(阴影部分均不通风).
下滑动且始终保持和AB平行的伸缩横杆,△EMN是随MN滑动而变化的三角通风窗(阴影部分均不通风). 如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形
如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形