��Ŀ����
����Ŀ���Ķ����в��ϣ��������Ӧ������
��ϣ���ļ���ѧ�Һ��������������������ۡ�һ���и�������������������֮��������Ĺ�ʽ������������ʽS��![]() ������a��b��c�������ε����߳���
������a��b��c�������ε����߳���![]() ��SΪ�����ε����������������֤��
��SΪ�����ε����������������֤��
���磺�ڡ�ABC�У�a��3��b��4��c��5����ô������������������㣺
��a��3��b��4��c��5
��![]() ��6
��6
��S��![]() ��
��![]() ��6
��6
��ʵ�ϣ�������֪�����ε����߳�����������������⣬�������ҹ�����ʱ����ѧ���ؾ���������ؾ��ع�ʽ�ȷ��������
�����������ϣ�����������⣺
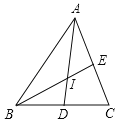
��ͼ���ڡ�ABC�У�BC��7��AC��8��AB��9
��1���ú���ʽ���ABC�������
��2����ͼ��AD��BEΪ��ABC��������ƽ���ߣ����ǵĽ���ΪI�����ABI�������
���𰸡���1��![]() ����2��
����2��![]() .
.
��������
��1�����ղ��ϸ����Ĺ�ʽ������ֵ���뼴����������
��2������I��IF��AB��IG��AC��IH��BC������ֱ�Ϊ��F��G��H�����ý�ƽ���ߵ����ʿ�֪IF��IH��IG�����õڣ�1�����������������IF��������������������ʽ���ABI���������.
�⣺��1����BC��7��AC��8��AB��9��
��![]()
![]()
�𣺡�ABC�����![]() ��
��
��2����ͼ������I��IF��AB��IG��AC��IH��BC������ֱ�Ϊ��F��G��H��
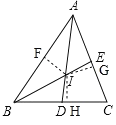
��AD��BE�ֱ�Ϊ��ABC�Ľ�ƽ���ߣ�
��IF��IH��IG��
��S��ABC��S��ABI+S��ACI+S��BCI��
��![]() ��9IF+8IF+7IF����
��9IF+8IF+7IF����![]()
���IF��![]()
��S��ABI��![]() ABFI��
ABFI��![]() ��9��
��9��![]() ��
��![]() ��
��

 �������ϵ�д�
�������ϵ�д�