题目内容
 在等腰梯形ABCD中,AD∥BC,BC=3,AD=1,∠B=45°,直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.①当AB=BE时,CF=
在等腰梯形ABCD中,AD∥BC,BC=3,AD=1,∠B=45°,直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.①当AB=BE时,CF=分析:平移一腰,根据等腰梯形上下底边的长度及底角度数求出腰长.①当AB=BE时,根据等腰三角形的性质先求出∠BEA的度数,再由平角的定义,等腰梯形的性质及三角形内角和定理求出∠FEC与∠CFE的度数,然后根据等腰三角形的判定得出CF=CE;②当AB=AE时,根据等腰三角形的性质得出∠BEA=∠B=45°,△ABE是等腰直角三角形,求出BE的长,则CE=BC-BE,再证△CEF是等腰直角三角形,从而得出CF=
CE;③EA=EB时,先证△ABE是等腰直角三角形,得出BE=
AB=1,则CE=BC-BE=2,再证点D与点F重合,△CDE是等腰直角三角形,从而得出CF=
CE.
| 2 |
| ||
| 2 |
| ||
| 2 |
解答: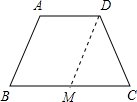 解:过点D作DM∥AB交BC于M,得到?ABDM和等腰△DMC.
解:过点D作DM∥AB交BC于M,得到?ABDM和等腰△DMC.
∴BM=AD=1,CM=BC-BM=3-1=2.
在△DMC中,∠DMC=∠C=∠B=45°,
∴∠MDC=90°,
∴△MDC是等腰直角三角形.
∴CD=DM=
CM=
,
∴AB=
.
①当AB=BE=
时,
∵∠B=45°,
∴∠BEA=67.5°,
∴∠FEC=180°-∠BEA-∠AEF=180°-67.5°-45°=67.5°,
∴∠CFE=180°-∠FEC-∠C=180°-67.5°-45°=67.5°,
∴CF=CE=BC-BE=3-
;
②当AB=AE=
时,
∵∠B=45°,
∴∠BEA=45°,∠BAE=90°,
∴BE=
AB=2,
∴CE=BC-BE=3-2=1.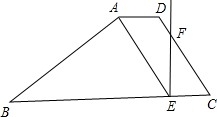
又∵∠FEC=180°-∠BEA-∠AEF=180°-45°-45°=90°,∠C=45°,
∴△CEF是等腰直角三角形,
∴CF=
CE=
;
③当EA=EB时,
∵∠B=45°,
∴∠BAE=∠B=45°,∠BEA=90°,
∴△ABE是等腰直角三角形,
∴BE=AE=
AB=1.
∵AD=1,∠DAE=90°,∠AED=∠AEF=45°,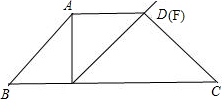
∴点D与点F重合.
在△CDE中,∠C=∠CED=45°,CE=BC-BE=3-1=2,
∴CF=
CE=
.
 解:过点D作DM∥AB交BC于M,得到?ABDM和等腰△DMC.
解:过点D作DM∥AB交BC于M,得到?ABDM和等腰△DMC.∴BM=AD=1,CM=BC-BM=3-1=2.
在△DMC中,∠DMC=∠C=∠B=45°,
∴∠MDC=90°,
∴△MDC是等腰直角三角形.
∴CD=DM=
| ||
| 2 |
| 2 |
∴AB=
| 2 |
①当AB=BE=
| 2 |
∵∠B=45°,
∴∠BEA=67.5°,
∴∠FEC=180°-∠BEA-∠AEF=180°-67.5°-45°=67.5°,

∴∠CFE=180°-∠FEC-∠C=180°-67.5°-45°=67.5°,
∴CF=CE=BC-BE=3-
| 2 |
②当AB=AE=
| 2 |
∵∠B=45°,
∴∠BEA=45°,∠BAE=90°,
∴BE=
| 2 |
∴CE=BC-BE=3-2=1.

又∵∠FEC=180°-∠BEA-∠AEF=180°-45°-45°=90°,∠C=45°,
∴△CEF是等腰直角三角形,
∴CF=
| 2 |
| 2 |
③当EA=EB时,
∵∠B=45°,
∴∠BAE=∠B=45°,∠BEA=90°,
∴△ABE是等腰直角三角形,
∴BE=AE=
| ||
| 2 |
∵AD=1,∠DAE=90°,∠AED=∠AEF=45°,

∴点D与点F重合.
在△CDE中,∠C=∠CED=45°,CE=BC-BE=3-1=2,
∴CF=
| ||
| 2 |
| 2 |
点评:本题主要考查了等腰三角形、等腰梯形的性质以及等腰直角三角形的性质和判定.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且 24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.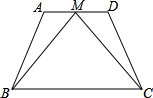 如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么?
如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么? 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.