题目内容
 如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=
如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=
- A.25°
- B.27°
- C.30°
- D.45°
B
分析:根据题意中的条件判定△ADB≌△CDB和△ADB≌△CDE,根据全等三角形的性质可得∠ABD=∠CBD和∠E=∠ABD,即:∠E=∠ABD=∠CBD,又因为∠ABC=∠ABD+∠CBD=54°,所以∠E=∠ABD=∠CBD= ×∠ABC,代入∠ABC的值可求出∠E的值.
×∠ABC,代入∠ABC的值可求出∠E的值.
解答:在△ADB和△CDB,
∵BD=BD,∠ADB=∠CDB=90°,AD=CD
∴△ADB≌△CDB,
∴∠ABD=∠CBD,
又∵∠ABC=∠ABD+∠CBD=54°,
∴∠ABD=∠CBD= ×∠ABC=27°.
×∠ABC=27°.
在△ADB和△EDC中,
∵AD=CD,∠ADB=∠EDC=90°,BD=ED,
∴△ADB≌△CDE,
∴∠E=∠ABD.
∴∠E=∠ABD=∠CBD=27°.
所以,本题应选择B.
点评:本题主要考查了全等三角形的判定和全等三角形的性质.通过全等证得∠ABD=∠CBD是解决本题的关键.
分析:根据题意中的条件判定△ADB≌△CDB和△ADB≌△CDE,根据全等三角形的性质可得∠ABD=∠CBD和∠E=∠ABD,即:∠E=∠ABD=∠CBD,又因为∠ABC=∠ABD+∠CBD=54°,所以∠E=∠ABD=∠CBD=
 ×∠ABC,代入∠ABC的值可求出∠E的值.
×∠ABC,代入∠ABC的值可求出∠E的值.解答:在△ADB和△CDB,
∵BD=BD,∠ADB=∠CDB=90°,AD=CD
∴△ADB≌△CDB,
∴∠ABD=∠CBD,
又∵∠ABC=∠ABD+∠CBD=54°,
∴∠ABD=∠CBD=
 ×∠ABC=27°.
×∠ABC=27°.在△ADB和△EDC中,
∵AD=CD,∠ADB=∠EDC=90°,BD=ED,
∴△ADB≌△CDE,
∴∠E=∠ABD.
∴∠E=∠ABD=∠CBD=27°.
所以,本题应选择B.
点评:本题主要考查了全等三角形的判定和全等三角形的性质.通过全等证得∠ABD=∠CBD是解决本题的关键.

练习册系列答案
相关题目
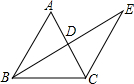 如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=( )
如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=( )| A、25° | B、27° | C、30° | D、45° |
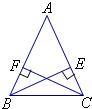 32、如图所示,BE⊥AC,CF⊥AB,垂足分别是E.F,若BE=CF,则图中全等三角形有( )
32、如图所示,BE⊥AC,CF⊥AB,垂足分别是E.F,若BE=CF,则图中全等三角形有( )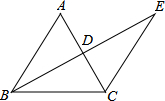 如图所示,BE⊥AC于点D,且AB=CB,BD=ED,若∠ABC=54°,则∠E=
如图所示,BE⊥AC于点D,且AB=CB,BD=ED,若∠ABC=54°,则∠E=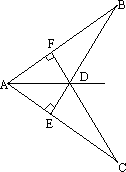
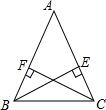 如图所示,BE⊥AC,CF⊥AB,垂足分别是E.F,若BE=CF,则图中全等三角形有
如图所示,BE⊥AC,CF⊥AB,垂足分别是E.F,若BE=CF,则图中全等三角形有