题目内容
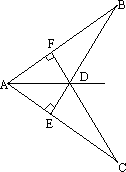
如图所示,BE⊥AC于E,CF⊥AB于F,BE,CF相交于点D,BD=CD,求证:AD平分∠BAC.
答案:
解析:
解析:
|
证明:因为BE⊥AC,CF⊥AB(已知), 所以∠BFD=∠CED=90°(垂直定义). 在△BFD和△CED中, 所以△BFD≌△CED(AAS). 所以DF=DE(全等三角形对应边相等). 又因为DF⊥AB,DE⊥AC, 所以AD平分∠BAC(到角的两边距离相等的点在这个角的平分线上). 分析:因为BE⊥AC,CF⊥AB,要证AD平分∠BAC,只需证明DF=DE即可,可从证明△BDF≌△CDE入手. |

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
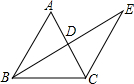 如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=( )
如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=( )| A、25° | B、27° | C、30° | D、45° |
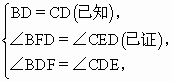
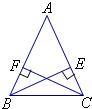 32、如图所示,BE⊥AC,CF⊥AB,垂足分别是E.F,若BE=CF,则图中全等三角形有( )
32、如图所示,BE⊥AC,CF⊥AB,垂足分别是E.F,若BE=CF,则图中全等三角形有( )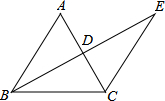 如图所示,BE⊥AC于点D,且AB=CB,BD=ED,若∠ABC=54°,则∠E=
如图所示,BE⊥AC于点D,且AB=CB,BD=ED,若∠ABC=54°,则∠E= 如图所示,BE⊥AC,CF⊥AB,垂足分别是E.F,若BE=CF,则图中全等三角形有
如图所示,BE⊥AC,CF⊥AB,垂足分别是E.F,若BE=CF,则图中全等三角形有