题目内容
【题目】小明和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1. 5倍.设两人出发x min后距出发点的距离为y m.图中折线段OBA表示小明在整个训练中y与x的函数关系,其中点A在x轴上,点B坐标为(2,480).
(1)点B所表示的实际意义是 ;
(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小明上坡平均速度的一半,那么两人出发后多长时间第一次相遇?

【答案】(1)、小明出发2分钟跑到坡顶,此时离坡脚480米;(2)、y=-360x+1200;(3)、2.5min.
【解析】
试题分析:(1)、根据函数图象得出点B的实际意义;(2)、首先求出上坡的速度,然后得出下坡的速度已经点A的坐标;利用待定系数法求出函数解析式;(3)、首先求出小刚上坡的速度,然后进行计算.
试题解析:(1)、小明出发2分钟跑到坡顶,此时离坡脚480米;
(2)、小明上坡的平均速度为480÷2=240(m/min) 则其下坡的平均速度为:240×1.5=360(m/min),
故回到出发点时间为2+480÷360=(min), ∴A点坐标为(![]() ,0),
,0),
设y=kx+b,将B(2,480)与A(![]() ,0)代入得:
,0)代入得: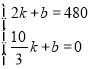 解得:
解得:![]()
∴y=-360x+1200.
(3)、小刚上坡的平均速度为240×0.5=120(m/min),小明的下坡平均速度为240×1.5=360(m/min),由图像得小明到坡顶时间为2分钟,
此时小刚还有480-2×120=240m没有跑完, 两人第一次相遇时间为2+240÷(120+360)=2.5(min).

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目

