题目内容
如图在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下的部分拼成一个梯形,分别计算这两个图形阴影部分面积,可以验证下面一个等式是( )


| A.(a+b)2=a2+2ab+b2 |
| B.(a-b)2=a2-2ab+b2 |
| C.a2-b2=(a+b)(a-b) |
D.a2+b2=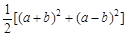 |
C
答:前图的阴影面积为:大正方形减去小正方形
= a2-b2
后图为等腰梯形:上底为b+b;下底为a+a;高为:a-b
所以面积为:(2a+2b)*(a-b)/2
即:(a+b)(a-b)
两面积相同所以可得等式为:a2-b2=(a+b)(a-b)
选C
= a2-b2
后图为等腰梯形:上底为b+b;下底为a+a;高为:a-b
所以面积为:(2a+2b)*(a-b)/2
即:(a+b)(a-b)
两面积相同所以可得等式为:a2-b2=(a+b)(a-b)
选C

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
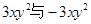
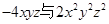
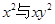
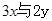
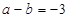 ,
,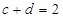 ,则
,则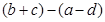 的值为( )
的值为( )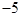
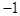
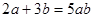



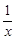 +
+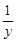 +
+ =0,那么x2+y2+z2的值为 。
=0,那么x2+y2+z2的值为 。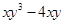 =_____________________.
=_____________________.