题目内容
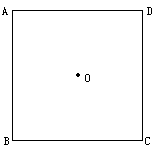
如图所示，在边长为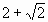
的正方形ABCD中，O为对角线交点，请作出正方形ABCD绕点O旋转45°后的图形，你能计算出这两个正方形重叠部分的面积吗？
答案：能
解析：
解析：
|
解：过 O作
，且OE＝OF＝OG＝OH＝OA再依次连结E，F，G，H得到四边形，从而四边形EFGH是正方形ABCD绕点O旋转45°的图形
因此应有 AR＝AP＝EP＝EQ＝DQ，设AP＝x所以 
故 
故 
因而旋转前后的正方形重叠部分面积为：
|
，所以x＝1
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
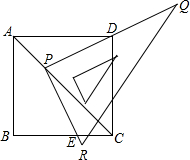移动，直角边PQ经过点D，另一直角边与射线BC交于点E．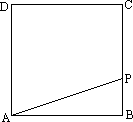
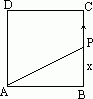
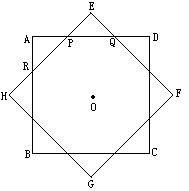
的正方形ABCD的一边BC上，有一点P从B点运动到C点．设PB＝x，图形APCD的面积为y，写出y与自变量x的函数关系式，并在直角坐标系系中画出它的图像．
的正方形ABCD的一边BC上，有一点P从点B运动到点C，设PB＝x，图形APCD的面积为y．
时，y等于多少？此时它表示的又是什么？
的正方形中，有四个斜边为
，直角边为
的全等直角三角形，你能利用这个图说明勾股定理吗？写出理由。