题目内容
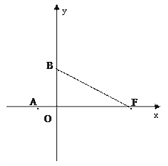
【题目】已知抛物线经过点A(-3, 0),F(8, 0),B(0, 4)三点.
(1)求抛物线解析式及对称轴.
(2)若点D在线段FB上运动(不与F,B重合),过点D作DC⊥轴于点C(x, 0),将△FCD沿CD向左翻折,点B对应点为点E, △CDE与△FBO重叠部分面积为S.
①试求出S与x之间的函数关系式,并写出自变量取值范围.
②是否存在这样的点C,使得△BDE为直角三角形,若存在,求出C点坐标,若不存在,请说明理由;
(3)抛物线对称轴上有一点M,平面内有一点N,若以A,B,M,N四点组成的四边形为菱形,求点N的坐标;

【答案】(1)![]() , 对称轴
, 对称轴![]() ;(2) ①
;(2) ①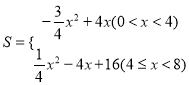 ;②存在,
;②存在, ![]() 或
或![]() ; (3)
; (3) 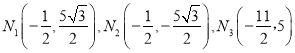 .
.
【解析】试题分析:(1)利用待定系数法即可求出;(2) ①C点的位置应分两种情况进行讨论,当C在OF的中点或在中点与F之间时,重合部分是△CDE;当C在OF的中点与O之间时,重合部分是梯形,就可以得到函数解析式.②分△BDE以点B为直角顶点和△BDE以点E为直角顶点,两种情况进行讨论.根据相似三角形的对应边的比相等,求出OE的长,就可以得到C点的坐标;(3)①AB为边,②AB为对角线,分两种情况分析讨论就能得到答案.
试题解析:
(1)设抛物线解析式为y=a(x+3)(x-8),把(0,4)代入得4=a×3×(-8),解得![]() ,
,
∴![]()
此时,抛物线的对称轴为:直线![]()
(2)①
②当∠BED=90°时,△BOE∽△ECD
∴![]() ,
,![]() ,
,
∴EO=2
∴EC=3
∴![]()
当∠EBD=90°时,△EOB∽△BOF
∴EO=2,
∴EC=(2+8)/2,
∴![]()
(3)①以AB为边,以B为圆心,AB为半径画圆交对称轴于![]() 两点,
两点,
![]() ,
,
由![]() 平移至
平移至![]() 得,
得,
![]() ,
,![]() ,
,
以A为圆心,AB为半径画圆,此时与对称轴没有交点,
故不存在.
②AB为对角线,直线AB的解析式为: ![]() ,
,
则AB的中垂线MN的解析式为: ![]() ,
,
当![]() 时 ,y=-1
时 ,y=-1
∴![]() ,
,![]() .
.
综上所述: ![]() ,
, ![]() ,
, ![]() .
.
点睛:此题综合考查了相似综合题,其中涉及到了待定系数法求二次函数的解析式、二次函数最值的求法,相似三角形的判定与性质以及多边形面积的求法等知识点. 解答此类关于函数的综合性应用题要善于设点,然后利用点与直线的关系或者点与其他函数的关系,然后把题中所有可能用到的点用只含一个未知数的方程表达出来.此题难度较大,注意掌握函数思想、分类讨论思想与树形结合思想的应用.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案