题目内容
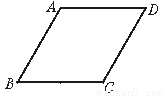
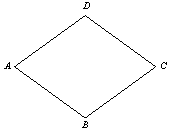
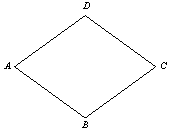
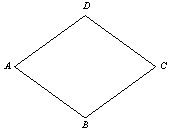
菱形ABCD中，如图，∠BAD=120°，AB=10cm，则AC=________cm，BD=________cm．
10 10
分析：连接AC，BD，则根据∠BAD=120°可证明△ABC为等边三角形，即AC=AB，解直角△AOB即可求得BO的值，即可求BD的值．
解答：
解：连接AC，BD，AC，BD交于点O，则AC⊥BD
（1）∵∠BAD=120°
∴∠ABC=60°，∵AB=BC
∴△ABC为等边三角形，即AC=AB=10cm，
（2）AB=AC=10cm，则OA=5cm，
则BO=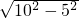
cm=5cm，
∴BD=10cm．
故答案为 10，10．
点评：本题考查了勾股定理的运用，考查了等边三角形的判定和边长相等的性质，本题中计算BO的值是解题的关键．
分析：连接AC，BD，则根据∠BAD=120°可证明△ABC为等边三角形，即AC=AB，解直角△AOB即可求得BO的值，即可求BD的值．
解答：
解：连接AC，BD，AC，BD交于点O，则AC⊥BD（1）∵∠BAD=120°
∴∠ABC=60°，∵AB=BC
∴△ABC为等边三角形，即AC=AB=10cm，
（2）AB=AC=10cm，则OA=5cm，
则BO=
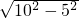cm=5cm，∴BD=10
cm．故答案为 10，10
．点评：本题考查了勾股定理的运用，考查了等边三角形的判定和边长相等的性质，本题中计算BO的值是解题的关键．
练习册系列答案
相关题目
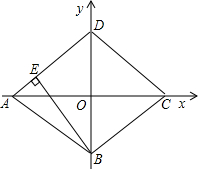已知直角坐标系中菱形ABCD的位置如图，C，D两点的坐标分别为（4，0），（0，3）．现有两动点P，Q分别从A，C同时出发，点P沿线段AD向终点D运动，点Q沿折线CBA向终点A运动，设运动时间为t秒．
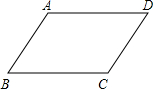菱形ABCD中，如图，∠BAD=120°，AB=10cm，则AC=
