题目内容
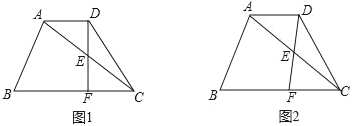
【题目】已知在梯形ABCD中,AD∥BC,AC=BC=10,cos∠ACB=![]() ,点E在对角线AC上(不与点A、C重合),∠EDC=∠ACB,DE的延长线与射线CB交于点F,设AD的长为x.
,点E在对角线AC上(不与点A、C重合),∠EDC=∠ACB,DE的延长线与射线CB交于点F,设AD的长为x.
(1)如图1,当DF⊥BC时,求AD的长;
(2)设EC=y,求y关于x的函数解析式,并直接写出定义域;
(3)当△DFC是等腰三角形时,求AD的长.
【答案】(1)AD=![]() ;(2)y=
;(2)y=![]() x2﹣
x2﹣![]() x+10(0<x≤10);(3)AD的长为6和
x+10(0<x≤10);(3)AD的长为6和![]() .
.
【解析】
(1)证明△ADC∽△DCE,利用ACCE=CD2=DF2+FC2=36+16a2=105a,即可求解;
(2)过点C作CH⊥AD交AD的延长线于点H,CD2=CH2+DH2=(ACsinα)2+(ACcosα﹣x)2,即可求解;
(3)分DF=DC、FC=DC、FC=FD三种情况,求解即可.
(1)设∠ACB=∠EDC=∠α=∠CAD,
∵cosα=![]() ,
,
∴sinα=![]() ,
,
过点A作AH⊥BC交于点H,
AH=ACsinα=6=DF,BH=2,

如图1,设:FC=4a,
∴cos∠ACB=![]() ,则EF=3a,EC=5a,
,则EF=3a,EC=5a,
∵∠EDC=∠α=∠CAD,∠ACD=∠ACD,
∴△ADC∽△DCE,
∴ACCE=CD2=DF2+FC2=36+16a2=105a,
解得:a=2或![]() (舍去a=2),
(舍去a=2),
AD=HF=10﹣2﹣4a=![]() ;
;
(2)过点C作CH⊥AD交AD的延长线于点H,
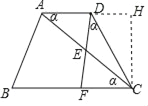
CD2=CH2+DH2=(ACsinα)2+(ACcosα﹣x)2,
即:CD2=36+(8﹣x)2,
由(1)得:ACCE=CD2,
即:y=![]() x2﹣
x2﹣![]() x+10(0<x≤10)…①,
x+10(0<x≤10)…①,
(3)①当DF=DC时,
∵∠ECF=∠FDC=α,∠DFC=∠DFC,
∴△DFC∽△CFE,∵DF=DC,
∴FC=EC=y,∴x+y=10,
即:10=![]() x2﹣
x2﹣![]() x+10+x,
x+10+x,
解得:x=6;
②当FC=DC,
则∠DFC=∠FDC=α,
则:EF=EC=y,DE=AE=10﹣y,
在等腰△ADE中,cos∠DAE=cosα= ,
,
即:5x+8y=80,
将上式代入①式并解得:x=![]() ;
;
③当FC=FD,
则∠FCD=∠FDC=α,而∠ECF=α≠∠FCD,不成立,
故:该情况不存在;
故:AD的长为6和![]() .
.