题目内容
如图,在直角坐标系中,⊙P的圆心P在x轴上,⊙P与x轴交于点E、F,与y 轴交于点C、D,且EO=1,CD=2
轴交于点C、D,且EO=1,CD=2
,又B、A两点的坐标分别为(0,m)、(5,0).
(1)当m=3时,求经过A、B两点的直线解析式;
(2)当B点在y轴上运动时,若直线AB与⊙P保持相交,求m的取值范围.
 轴交于点C、D,且EO=1,CD=2
轴交于点C、D,且EO=1,CD=2| 3 |
(1)当m=3时,求经过A、B两点的直线解析式;
(2)当B点在y轴上运动时,若直线AB与⊙P保持相交,求m的取值范围.
(1)当m=3时,B的坐标为(0,3).
设经过A、B两点的直线解析式为y=kx+b,由题意得
,
解得
,
∴经过A、B两点的直线解析式为y=-
x+3;
(2)假设当B点移到B'时,直线AB'与⊙P相切于点H,连接PH、PD,设圆的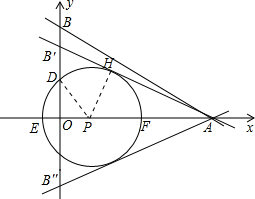 半径为x,
半径为x,
∵EO=1,CD=2
,
∴PD2=OD2+OP2,
即x2=(
)2+(x-1)2,解得x=2;
∵OA=5,
∴AP=OA-OP=5-1=4,
在Rt△APH中,PH=2,AP=4,
∴∠PAH=30°,
在Rt△AEB'中,OB'=tan30°×5=
;
同理OB''=-
,
∴若直线AB与⊙P保持相交,m的取值范围是-
<m<
.
设经过A、B两点的直线解析式为y=kx+b,由题意得
|
解得
|
∴经过A、B两点的直线解析式为y=-
| 3 |
| 5 |
(2)假设当B点移到B'时,直线AB'与⊙P相切于点H,连接PH、PD,设圆的
 半径为x,
半径为x,∵EO=1,CD=2
| 3 |
∴PD2=OD2+OP2,
即x2=(
| 3 |
∵OA=5,
∴AP=OA-OP=5-1=4,
在Rt△APH中,PH=2,AP=4,
∴∠PAH=30°,
在Rt△AEB'中,OB'=tan30°×5=
| 5 |
| 3 |
| 3 |
同理OB''=-
| 5 |
| 3 |
| 3 |
∴若直线AB与⊙P保持相交,m的取值范围是-
| 5 |
| 3 |
| 3 |
| 5 |
| 3 |
| 3 |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目




