题目内容
【题目】如图,∠B、∠D的两边分别平行。

(1)在图①中,∠B与∠D的数量关系为相等相等。
(2)在图②中,∠B与∠D的数量关系为互补互补。
(3)用一句话归纳的结论为如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补。
试分别说明理由。
【答案】(1)相等(2)互补(3)如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补。
【解析】
(1)根据平行线的性质得出∠CME=∠D,∠B=∠CME,即可解答
(2)根据平行线的性质得出∠BND+∠D=180°,∠B=∠BND,即可解答
(3)根据平行线的性质可知:如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补。
相等,理由是:
如图(1)∵BE∥DF,
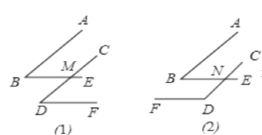
∴∠CME=∠D,
∵AB∥DC,
∴∠B=∠CME,
∴∠B=∠D;
互补,理由是:
如图(2)∵BE∥DF,
∴∠BND+∠D=180°,
∵AB∥DC,
∴∠B=∠BND,
∴∠B+∠D=180°.
(3)如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补。

练习册系列答案
相关题目