题目内容
已知:如图,在正方形ABCD中,点G是BC延长线一点,连接AG,分别交BD、CD于点E、F.(1)求证:∠DAE=∠DCE;
(2)当CG=CE时,试判断CF与EG之间有怎样的数量关系?并证明你的结论.
(3)在(2)的条件下,求
 的值.
的值.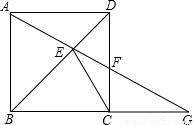
【答案】分析:(1)根据四边形ABCD是正方形,得到AD=CD,∠ADE=∠CDE,又知DE为公共边,可以推出△ADE≌△CDE,利用全等三角形的性质得到∠DAE=∠DCE.
(2)根据正方形的性质及CG=CE,证出CF=EF,再求出∠G=30°,判断出CF= FG,从而得到
FG,从而得到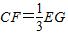 .
.
(3)设CF=x,则EF=CF=x,FG=2CF=2x,利用△ADE≌△CDE,得到AE=CE=CG=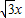 ,AF=AE+EF=
,AF=AE+EF= ,由于△ADF∽△GCF,利用相似三角形的性质求出
,由于△ADF∽△GCF,利用相似三角形的性质求出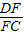
的值.
解答: (1)证明:∵四边形ABCD是正方形,
(1)证明:∵四边形ABCD是正方形,
∴AD=CD,∠ADE=∠CDE.
∵DE=DE,
∴△ADE≌△CDE.
∴∠DAE=∠DCE.
(2) .
.
证明:∵四边形ABCD是正方形,
∴AD∥BC,∠DCB=90°
∴∠DAE=∠G.
∴∠DCE=∠G.
∵CG=CE,
∴∠1=∠G.
∴∠DCE=∠1.
∴CF=EF.
∵∠2=∠1+∠DCE=2∠1=2∠G,
又∵∠DCG=180°-∠DCB=90°,
∴∠G=30°,
∴ .
.
∴ .
.
(3)解:设CF=x,则EF=CF=x,FG=2CF=2x.
在Rt△CFG中, .
.
∵△ADE≌△CDE,
∴AE=CE=CG= .
.
∴AF=AE+EF= .
.
∵AD∥BC,
∴△ADF∽△GCF,
∴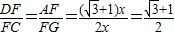 .
.
点评:本题考查了相似三角形的性质、全等三角形的性质、正方形的性质,综合性较强,要从图中找到相关的量,注意挖掘隐含条件.
(2)根据正方形的性质及CG=CE,证出CF=EF,再求出∠G=30°,判断出CF=
 FG,从而得到
FG,从而得到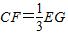 .
.(3)设CF=x,则EF=CF=x,FG=2CF=2x,利用△ADE≌△CDE,得到AE=CE=CG=
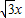 ,AF=AE+EF=
,AF=AE+EF= ,由于△ADF∽△GCF,利用相似三角形的性质求出
,由于△ADF∽△GCF,利用相似三角形的性质求出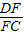
的值.
解答:
 (1)证明:∵四边形ABCD是正方形,
(1)证明:∵四边形ABCD是正方形,∴AD=CD,∠ADE=∠CDE.
∵DE=DE,
∴△ADE≌△CDE.
∴∠DAE=∠DCE.
(2)
 .
.证明:∵四边形ABCD是正方形,
∴AD∥BC,∠DCB=90°
∴∠DAE=∠G.
∴∠DCE=∠G.
∵CG=CE,
∴∠1=∠G.
∴∠DCE=∠1.
∴CF=EF.
∵∠2=∠1+∠DCE=2∠1=2∠G,
又∵∠DCG=180°-∠DCB=90°,
∴∠G=30°,
∴
 .
.∴
 .
.(3)解:设CF=x,则EF=CF=x,FG=2CF=2x.
在Rt△CFG中,
 .
.∵△ADE≌△CDE,
∴AE=CE=CG=
 .
.∴AF=AE+EF=
 .
.∵AD∥BC,
∴△ADF∽△GCF,
∴
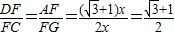 .
.点评:本题考查了相似三角形的性质、全等三角形的性质、正方形的性质,综合性较强,要从图中找到相关的量,注意挖掘隐含条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
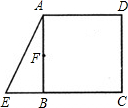 已知:如图,在正方形ABCD中,E是CB延长线上一点,EB=
已知:如图,在正方形ABCD中,E是CB延长线上一点,EB=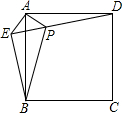 已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=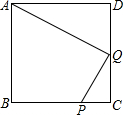 已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似?
已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似? 、CE、CB于点F、H、G,交AB的延长线于点P.
、CE、CB于点F、H、G,交AB的延长线于点P. 已知:如图,在正方形ABCD中,E、F分别是AD、CD的中点.
已知:如图,在正方形ABCD中,E、F分别是AD、CD的中点.