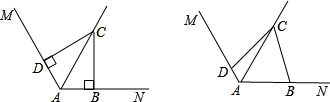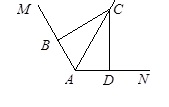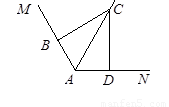题目内容
已知∠MAN,AC平分∠MAN。

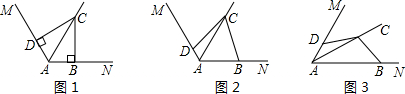
(1)在图(1)中,若∠MAN=120°,∠ABC=∠ADC=90°,则AB+AD____AC;(填写“>”“<”或“=”)
(2)在图(2)中,若∠MAN=120°,∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)在图(3)中:
①若∠MAN=60°,∠ABC+∠ADC=180°,判断AB+AD与AC的数量关系,并说明理由;
②若∠MAN=α(0°<α<180°),∠ABC+∠ADC=180°,则AB+AD=____AC。(用含α的三角函数表示,直接写出结果,不必证明)
(2)在图(2)中,若∠MAN=120°,∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
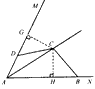
(3)在图(3)中:
①若∠MAN=60°,∠ABC+∠ADC=180°,判断AB+AD与AC的数量关系,并说明理由;
②若∠MAN=α(0°<α<180°),∠ABC+∠ADC=180°,则AB+AD=____AC。(用含α的三角函数表示,直接写出结果,不必证明)
| 解:(1)=; | |
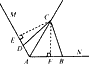
| (2)仍然成立,理由: 如图(1)过C作CE⊥AM于E,CF⊥AN于F,则∠CEA=∠CFA=90°, ∵AC平分∠MAN,∠MAN=120°, ∴∠MAC=∠NAC=60°, 又∵AC=AC, ∴△AEC≌△AFC ∴AE=AF,CE=CF ∵在Rt△CEA中,∠EAC=60° ∴∠ECA=30° ∴AC=2AE ∴AE+AF=2AE=AC, ∴ED+DA+AE=AC, ∵∠ABC+∠ADC=180°,∠CDE+∠ADC=180°, ∴∠CDE=∠CBF, 又∵CE=CF,∠CED=∠CFB, ∴△CED≌△CFB, ∴ED=FB, ∴FB+DA+AF=AC, ∴AB+AD=AC; |
 |
(3)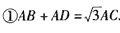 理由:如图(2)方法同(2)可证△AGC≌△AHC ∴AG=AH, ∵∠MAN=60°, ∴∠GAC=∠HAC=30°, ∴AG=AH=  , ,∴AG+AH=  , ,∴GD+DA+AH=  ,方法同(2)可证△GDC≌△HBC, ,方法同(2)可证△GDC≌△HBC,∴DG=HB, ∴HB+DA+AH= 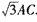 , ,∴AD+AB= 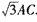 ; ;②2cos  。 。 |
 |

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目