题目内容
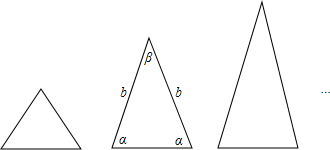
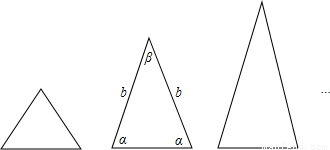
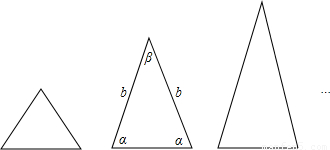
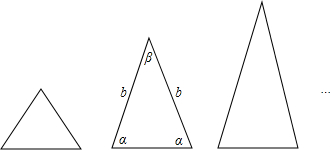
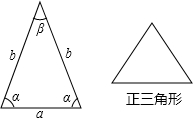
如图,等腰三角形与正三角形的形状有着差异,我们把它与正三角形的接近程度称为等腰三角形的“正度”,在研究“正度”时,应符合下面四个条件:①“正度”的值是非负数;②“正度”值越小,表示等腰三角形越接近正三角形;③相似的等腰三角形“正度”要相等;④正三角形的“正度”是0.例如:
设等腰三角形的底和腰分别为a,b,底角和顶角分别为α,β.
可用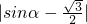 表示等腰三角形的“正度”,
表示等腰三角形的“正度”,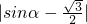 的值越小,α越接近60°,表示等腰三角形越接近正三角形,且当两个等腰三角形相似时,它们的底角相等,显然,它们的“正度”
的值越小,α越接近60°,表示等腰三角形越接近正三角形,且当两个等腰三角形相似时,它们的底角相等,显然,它们的“正度”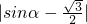 也相等,当α=60°时,
也相等,当α=60°时,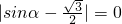 .
.
而如果用 表示等腰三角形的“正度”,就不符合要求,因为此时正三角形的正度是1!
表示等腰三角形的“正度”,就不符合要求,因为此时正三角形的正度是1!
解答下列问题:
甲同学认为:可用|a-b|表示等腰三角形的“正度”,|a-b|的值越小,表示等腰三角形越接近正三角形;
乙同学认为:可用|α-β|表示等腰三角形的“正度”,|α-β|的值越小,表示等腰三角形越接近正三角形.
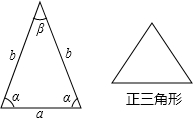 (1)他们的说法合理吗?为什么?
(1)他们的说法合理吗?为什么?
(2)对你认为不合理的方案加以改进,使其合理;
(3)请你再给出一种衡量等腰三角形“正度”的合理的表达式,并说明理由.
解:(1)同学乙的方案较为合理.
因为|α-β|的值越小,α与β越接近60°,
因而该等腰三角形越接近于正三角形,且能保证相似三角形的“正度”相等.
同学甲的方案不合理,不能保证相似三角形的“正度”相等.
如:边长为4,4,2和边长为8,8,4的两个等腰三角形相似,但|2-4|=2≠|4-8|=4.
(2)对同学甲的方案可改为用 ,
,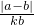 等(k为正数)来表示“正度”.
等(k为正数)来表示“正度”.
(3)还可用|α-60°|,|β-60°|,|α+β-120°|, 等来表示“正度”.
等来表示“正度”.
分析:(1)将甲乙两同学的推测进行推理,若代入特殊值不成立,则推理不成立.
(2)对同学甲的方案可改为用 ,
,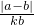 等(k为正数)来表示“正度”.
等(k为正数)来表示“正度”.
(3)还可用|α-60°|,|β-60°|,|α+β-120°|, 等来表示“正度”.
等来表示“正度”.
点评:本题考查了相似三角形的应用、等腰三角形的性质及解直角三角形的知识,此题是一道开放性问题,体现了探索发现的过程:发现问题,作出假设,进行验证,加以证明.
因为|α-β|的值越小,α与β越接近60°,
因而该等腰三角形越接近于正三角形,且能保证相似三角形的“正度”相等.
同学甲的方案不合理,不能保证相似三角形的“正度”相等.
如:边长为4,4,2和边长为8,8,4的两个等腰三角形相似,但|2-4|=2≠|4-8|=4.
(2)对同学甲的方案可改为用
 ,
,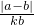 等(k为正数)来表示“正度”.
等(k为正数)来表示“正度”.(3)还可用|α-60°|,|β-60°|,|α+β-120°|,
 等来表示“正度”.
等来表示“正度”.分析:(1)将甲乙两同学的推测进行推理,若代入特殊值不成立,则推理不成立.
(2)对同学甲的方案可改为用
 ,
,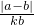 等(k为正数)来表示“正度”.
等(k为正数)来表示“正度”.(3)还可用|α-60°|,|β-60°|,|α+β-120°|,
 等来表示“正度”.
等来表示“正度”.点评:本题考查了相似三角形的应用、等腰三角形的性质及解直角三角形的知识,此题是一道开放性问题,体现了探索发现的过程:发现问题,作出假设,进行验证,加以证明.

练习册系列答案
相关题目
 (1)他们的说法合理吗?为什么?
(1)他们的说法合理吗?为什么?