题目内容
【题目】某少数民族的刺绣有着悠久的历史,如图![]() 为她们剌绣最简单的四个图案,这些图案都是由小正方形构成的,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),研究发现第
为她们剌绣最简单的四个图案,这些图案都是由小正方形构成的,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),研究发现第![]() 个图案中共有
个图案中共有![]() 个;小正方形.(
个;小正方形.(![]() 为整数,且
为整数,且![]() )
)
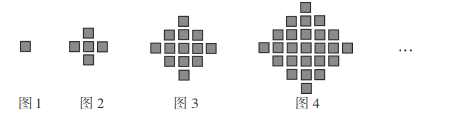
(1)请写出第![]() 个图案中有____个小正方形;
个图案中有____个小正方形;
(2)猜想第![]() 个图案和第
个图案和第![]() 个图案中小正方形个数之差为
个图案中小正方形个数之差为
(3)证明(2)中的猜想.
【答案】(1)41;(2)4n;(3)见解析.
【解析】
(1)首先观察给出的四个图,可以得出正方体的个数分别为![]() ,
,![]() ,
,![]()
![]() ,
,![]() 总结一般性的规律,将一般性数列转化为特殊的数列再求解.
总结一般性的规律,将一般性数列转化为特殊的数列再求解.
(2)根据(1)得出的一般规律,可写出第![]() 个图案中正方形的个数,再与第
个图案中正方形的个数,再与第![]() 个图案中正方形的个数做差即可得解.
个图案中正方形的个数做差即可得解.
(3)利用数列的求和公式可得第![]() 个图案中正方形的个数是:
个图案中正方形的个数是:![]() ,利用此规律可写出第
,利用此规律可写出第![]() 个图案中正方形的个数是
个图案中正方形的个数是![]() ,再让它们做差即可得证.
,再让它们做差即可得证.
(1)∵第一个图案中正方形的个数是:![]()
第二个图案中正方形的个数是:![]()
第三个图案中正方形的个数是:![]()
第四个图案中正方形的个数是:![]()
![]()
第![]() 个图案中正方形的个数是:
个图案中正方形的个数是:![]()
∴第五个图案中正方形的个数是:![]()
故答案是:![]()
(2)∵由(1)可知第![]() 个图案中正方形的个数是:
个图案中正方形的个数是:![]()
第![]() 个图案中正方形的个数是:
个图案中正方形的个数是:![]()
∴第![]() 个图案和第
个图案和第![]() 个图案中小正方形个数之差为
个图案中小正方形个数之差为![]()
∴第![]() 个图案和第
个图案和第![]() 个图案中小正方形个数之差为
个图案中小正方形个数之差为![]()
故答案是:![]()
(3)证明:根据题意,得第![]() 个图案中正方形的个数为
个图案中正方形的个数为
![]() .
.
![]() .
.
![]() .
.
![]() 第
第![]() 个图案和第
个图案和第![]() 个图案中正方形个数之差为
个图案中正方形个数之差为
![]()

练习册系列答案
相关题目