题目内容
若直角三角形的两条直角边的长分别是3和4，则斜边上的中线长为分析：根据勾股定理求出AB，根据直角三角形斜边上中线求出CD=
AB即可．
| 1 |
| 2 |
解答：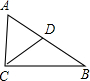
解：∵∠ACB=90°，AC=3，BC=4，由勾股定理得：AB=
=5，
∵CD是△ABC中线，
∴CD=
AB=
×5=2.5，
故答案为：2.5．
解：∵∠ACB=90°，AC=3，BC=4，由勾股定理得：AB=| AC2+BC2 |
∵CD是△ABC中线，
∴CD=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为：2.5．
点评：本题主要考查对勾股定理，直角三角形斜边上的中线等知识点的理解和掌握，能推出CD=
AB是解此题的关键．
| 1 |
| 2 |
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
，且
的两条直角边分别是水平和竖直状态，那么
的两条直角边也一定分别是水平和竖直状态
，
，那么
下列说法正确的是（ ）
A．若  ，且 的两条直角边分别是水平和竖直状态，那么 的两条直角边也一定分别是水平和竖直状态 |
B．如果 ， ，那么 |
| C．有一条公共边，而且公共边在每个三角形中都是腰的两个等腰三角形一定全等 |
| D．有一条相等的边，而且相等的边在每个三角形中都是底边的两个等腰三角形全等 |