题目内容
【题目】如图，是按规律摆放在墙角的一些小正方体，从上往下分别记为第一层，第二层，第三层…第n层…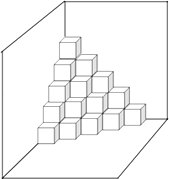 
（1）第三层有个小正方体．
（2）从第四层至第六层（含第四层和第六层）共有个小正方体．
（3）第n层有个小正方体．
（4）若每个小正方体边长为a分米，共摆放了n层，则要将摆放的小正方体能看到的表面部分涂上防锈漆，则防锈漆的总面积为分米2 ．
【答案】
（1）6
（2）46
（3）
（4）
n（n+1）
【解析】解：（1）第1层，共1个小正方体，
第2层正方体的个数为1+2=3，
第3层正方体的个数为：1+2+3=6．
所以答案是：6．（2）第4层正方体的个数为：10，
第5层正方体的个数为：15，
第6层正方体的个数为：21，
所以从第三层至第六层（含第三层和第六层）共有：10+15+21=46．
所以答案是：46．（3）根据（1）相应规律，可得第n层正方体的个数为1+2+3+…+n= ；（4）共摆放n层，则靠墙小正方形的面的个数：2×（1+2+3+…+n）=n（n+1），
地面接触小正方形的面的个数：1+2+3+…+n= ，
所以靠墙及地面的部分涂上防锈漆的面积为：[n（n+1）+ ]×a2= n（n+1）分米2 ．
所以答案是：（1）6；（2）41；（3） ；（4） n（n+1）．
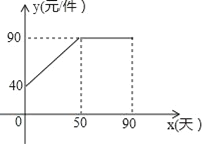
【题目】九年级某班数学兴趣小组经过市场调查整理出某种商品在第x天（1≤x≤90，且x为整数）的售价与销售量的相关信息如下．已知商品的进价为30元/件，设该商品的售价为y（单位：元/件），每天的销售量为p（单位：件），每天的销售利润为w（单位：元）．
时间x（天） | 1 | 30 | 60 | 90 |
每天销售量p（件） | 198 | 140 | 80 | 20 |
（1）求出w与x的函数关系式；
（2）问销售该商品第几天时，当天的销售利润最大？并求出最大利润；
（3）该商品在销售过程中，共有多少天每天的销售利润不低于5600元？请直接写出结果．
