Question

【题目】在平面直角坐标系中，抛物线y＝﹣x2+x+4的图象与x轴交于B，C两点（B在C的左侧），与y轴交于点A．

（1）求出点A，B，C的坐标．

（2）在抛物线上有一动点P，抛物线的对称轴上有另一动点Q，若以B，C，P，Q为顶点的四边形是平行四边形，直接写出点P的坐标．

（3）向右平移抛物线，使平移后的抛物线恰好经过△ABC的外心，求出平移后的抛物线的解析式．

Answer 1

【答案】（1）A（0，4），B（﹣2，0），C（8，0）；（2）P（3，）或（﹣7，﹣）或（13，﹣）；（3）y＝﹣+4x﹣

【解析】

（1）分别令x＝0和y＝0代入可求得点A，B，C的坐标；

（2）利用配方法求出抛物线的顶点坐标，分三种情况：当P在x轴的上方时，即为抛物线的顶点P（3，）；当P在x轴的下方时，有两种情况：①当P在抛物线对称轴的左侧时，如图2，②当P在抛物线对称轴的右侧时，如图3，根据PQ＝BC＝10，求出横坐标后再求纵坐标；

（3）通过证明△AOB∽△COA，得△ABC是直角三角形，得△ABC的外心E的坐标为（3，0），则抛物线向右平移5个单位，由此写出平移后的抛物线的解析式．

解：（1）当x＝0时，y＝4，

∴与y轴交点A（0，4），

当y＝0时，﹣x2+x+4＝0，

解得：x＝﹣2或8，

∴B（﹣2，0），C（8，0）；

（2）y＝﹣x2+x+4＝﹣（x﹣3）2+，

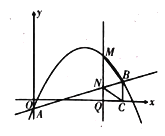
当P在x轴的上方时，即为抛物线的顶点P（3，）时，可以构成平行四边形BPCQ，如图1，

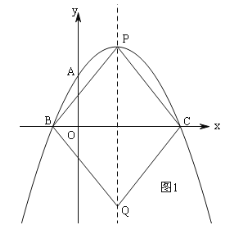
当P在x轴的下方时，

∵BC＝2+8＝10，

若四边形BPCQ为平行四边形，则BC∥PQ，BC＝PQ＝10，

有两种情况：①当P在抛物线对称轴的左侧时，如图2，

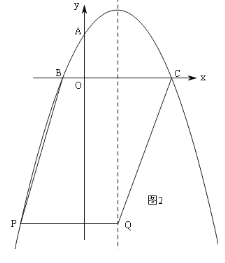
∴点P的横坐标为﹣7，

当x＝﹣7时，y＝﹣×（﹣7）2+×（﹣7）+4＝﹣，

此时P（﹣7，﹣）；

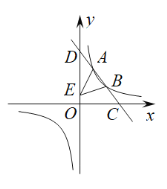
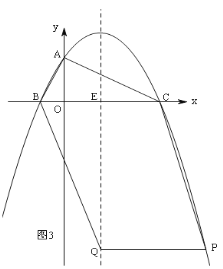
②当P在抛物线对称轴的右侧时，如图3，

∴点P的横坐标为13，

当x＝13时，y＝﹣×132+×13+4＝﹣，

此时P（13，﹣）；

综上所述，点P的坐标为P（3，）或（﹣7，﹣）或（13，﹣）；

（3）如图3，

∵A（0，4）、B（﹣2，0）、C（8，0）

∴OA＝4，OB＝2，OC＝8，

∴

∴，

∵∠AOB＝∠AOC＝90°，

∴△AOB∽△COA，

∴∠BAO＝∠ACO，

∵∠ACO+∠OAC＝90°，

∴∠BAO+∠OAC＝90°，

∴∠BAC＝90°，

∴△ABC是直角三角形，

∴△ABC的外心就是斜边BC的中点E，

∵BC＝10，

∴BC的中点E的坐标为（3，0），

即平移后的解析式经过E（3，0），

∴相当于把原抛物线向右平移5个单位，

∴平移后的解析式为：y＝﹣（x﹣3﹣5）2+＝﹣+4x﹣．