题目内容
【题目】如图,把一张边长为10cm的正方形纸板的四周各剪去一个边长为xcm的小正方形,再折叠成一个无盖的长方体盒子.
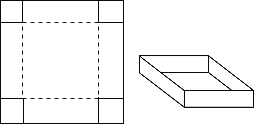
(1)当长方体盒子的底面积为81cm2时,求所剪去的小正方形的边长.
(2)设所折叠的长方体盒子的侧面积为S,求S与x的函数关系式,并写出x的取值范围.
(3)长方体盒子的侧面积为S的值能否是60cm2,若能,请求出x的值;若不能,请说明理由.
【答案】(1) 所剪去的小正方形的边长为0.5cm;(2) S与x的函数关系式为S=﹣8x2+40x,x的取值范围为0<x<5;(3) 不能.理由见解析
【解析】
(1)根据底面积是边长(10-2x)cm的正方形,即可求解;
(2)侧面积是四个面积相等的小长方形,列出二次函数即可;
(3)根据(2)所得函数关系式,将S=60代入解方程即可说明.
(1)根据题意,得
(10﹣2x)2=81
解得x1=0.5,x2=9.5(不符合题意,舍去)
答:所剪去的小正方形的边长为0.5cm.
(2)根据题意,得
S=4x(10﹣2x)
=﹣8x2+40x(0<x<5)
答:S与x的函数关系式为S=﹣8x2+40x,x的取值范围为0<x<5.
(3)答:不能.理由如下:
﹣8x2+40x=60,
整理得2x2﹣5x+15=0
∵△=25﹣120=﹣95<0,
∴此方程无解,
答:长方体盒子的侧面积为S的值不能是60cm2.

练习册系列答案
相关题目