题目内容
已知：关于x的一元二次方程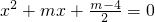
．
（1）求证：不论m为何值时，方程总有两个不相等的实数根；
（2）若方程的两个实数根为x1和x2，满足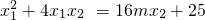
，且x1＜-x2，求m的值．
解：（1）证明：△=m2-4×1×
=m2-2m+8=（m-1）2+7．
∵（m-1）2≥0
∴（m-1）2+7＞0，
∴△＞0
∴不论m为何值时，方程总有两个不相等的实数根．
（2）∵x1和x2是方程x2+mx+=0的两个实数根，
∴
+mx1+
=0，
x1+x2=-m，x1+x2=
∴=-mx1-．
∵16+4x1x2=16mx2+25
∴16（-mx1-）+4x1x2-16mx2-25=0，
整理，得-16m（x1+x2）+4x1x2-8m+7=0
-16m（-m）+4×-8m+7=0
16m2-6m-1=0
（2m-1）（8m+1）=0，m=
或m=-
∵x1＜-x2
∴x1+x2=-m＜0．
∴m＞0，
∴m=．
分析：（1）首先利用含m的代数式表示出判别式△，然后把△进行配方，即可判断；
（2）利用一元二次方程的根与系数的关系以及方程的根的定理，把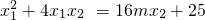变化成关于m的方程，解方程即可求得m的值．
点评：本题考查了一元二次方程的根与系数的关系，利用含m的代数式正确对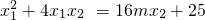进行变形是关键．
=m2-2m+8=（m-1）2+7．∵（m-1）2≥0
∴（m-1）2+7＞0，
∴△＞0
∴不论m为何值时，方程总有两个不相等的实数根．
（2）∵x1和x2是方程x2+mx+
=0的两个实数根，∴
+mx1+=0，x1+x2=-m，x1+x2=
∴
=-mx1-．∵16
+4x1x2=16mx2+25∴16（-mx1-
）+4x1x2-16mx2-25=0，整理，得-16m（x1+x2）+4x1x2-8m+7=0
-16m（-m）+4×
-8m+7=016m2-6m-1=0
（2m-1）（8m+1）=0，m=
或m=-∵x1＜-x2
∴x1+x2=-m＜0．
∴m＞0，
∴m=
．分析：（1）首先利用含m的代数式表示出判别式△，然后把△进行配方，即可判断；
（2）利用一元二次方程的根与系数的关系以及方程的根的定理，把
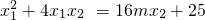变化成关于m的方程，解方程即可求得m的值．点评：本题考查了一元二次方程的根与系数的关系，利用含m的代数式正确对
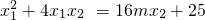进行变形是关键． 
练习册系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目