题目内容
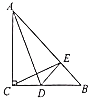
【题目】已知△ABC中,AB=AC,点D,E分别在直线AB,BC上,且∠DEC=∠DCE.
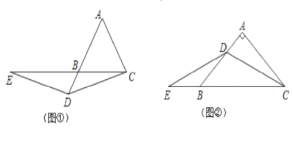
(1)如图①,若点D在线段AB的延长线上,∠A=60°,求证:EB=AD;
(2)如图②,若点D在线段AB上,∠A=90°,求证:EB=![]() AD;
AD;
(3)在(2)的条件下,若CD平分∠ACB,P是线段CD上任意一点,点Q,P关于BC对称,且BE=2,请直接写出△BPQ周长的最小值。
【答案】(1)见解析;(2)见解析;(3)4+2![]()
【解析】
(1)过D点作BC的平行线交AC的延长线于点F.可得等边三角形△ADF,再证明△DBE≌△CFD.可得BE=DF=AD;
(2)过D点作BC的平行线交AC于点G,只要证明△DBE≌△CGD即可解决问题;
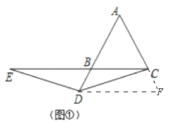
(3)如图③中,作PE⊥AC于E.只要证明△PBQ的周长=PB+BQ+PQ=2(PB+PH),由∠PCH=∠PCF,PH⊥CH,PE⊥CE,推出PH=PE,推出PB+PH=PB+PE,根据垂线段最短可知:当P与D重合,E与A重合时,PB+PE的值最小;
(1)证明:过D点作BC的平行线交AC的延长线于点F.
∵△ABC是等腰三角形,∠A=60°,
∴△ABC是等边三角形.∴∠ABC=60°,
∵DF∥BC,
∴∠ADF=∠ABC=60°,
∴△ADF是等边三角形。
∴AD=DF,∠AFD=60°,
∵∠DBE=∠ABC=60°,
∴∠DBE=∠AFD.
∵∠FDC=∠DCE,∠DCE=∠DEC,
∴∠FDC=∠DEC,ED=CD.
∴△DBE≌△CFD.
∴BE=DF,∴BE=AD.
(2)证明:过D点作BC的平行线交AC于点G,
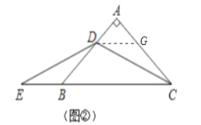
∵△ABC是等腰三角形,∠A=90°,
∴∠ABC=∠ACB=45°,
∴∠DBE=180°45°=135°,
∵DG∥BC,∴∠GDC=∠DCE,
∠DGC=180°45°=135°,
∴∠DBE=∠DGC,
∵∠DCE=∠DEC,
∴ED=CD,∠DEC=∠GDC,
∴△DBE≌△CGD,
∴BE=GD,
∵∠ADG=∠ABC=45°,∠A=90°,
∴△ADG是等腰直角三角形。
∴DG=![]() AD,
AD,
∴BE=![]() AD.
AD.
(3)如图③中,作PE⊥AC于E.
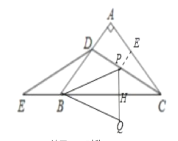
∵P、Q关于BC对称,
∴PB=BQ,PH=QH,
∴△PBQ的周长=PB+BQ+PQ=2(PB+PH),
∵∠PCH=∠PCF,PH⊥CH,PE⊥CE,
∴PH=PE,
∴PB+PH=PB+PE,
当P与D重合,E与A重合时,PB+PE的值最小,
∵BE=![]() AD,BE=2,
AD,BE=2,
∴AD=![]() ,
,
∵∠E=∠DCB=22.5°,∠ABC=∠E+∠BDE=45°,
∴∠E=∠BDE=22.5°,
∴BD=BE=2,
∴PB+PE的最小值为2+![]() ,
,
∴△PBQ的周长的最小值为4+2![]() .
.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】![]() 开通了,中国联通公布了资费标准,其中包月
开通了,中国联通公布了资费标准,其中包月![]() 元时,超出部分国内拨打
元时,超出部分国内拨打![]() 元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.
元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.
时间/分 | 1 | 2 | 3 | 4 | 5 | … |
电话费/元 | 0.36 | 0.72 | 1.08 | 1.44 | 1.80 | … |
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用![]() 表示超出时间,
表示超出时间,![]() 表示超出部分的电话费,那么
表示超出部分的电话费,那么![]() 与
与![]() 的关系式是什么?
的关系式是什么?
(3)如果打电话超出![]() 分钟,需多付多少电话费?
分钟,需多付多少电话费?
(4)某次打电话的费用超出部分是![]() 元,那么小明的爸爸打电话超出几分钟?
元,那么小明的爸爸打电话超出几分钟?