题目内容
△ABC的一边长为5，另两边长恰是方程2x2-12x+m=0的两个根，求m的取值范围．
解：由根与系数的关系可得：x1+x2=6，x1•x2=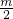
，
又有三角形的三边关系可得：|x1-x2|＜5，
则（x1-x2）2＜25，
即（x1+x2）2-4x1•x2＜25，
即：36-2m＜25
解得：m＞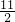
；
既然方程有两个实根，则△≥0，
解得m≤18．
故本题答案为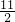：＜m≤18．
分析：根据一元二次方程的根与系数的关系及三角形的三边关系可得到（x1-x2）2＜25，把两根之积与两根之和代入（x1-x2）2的变形中，可求得m的取值范围，再由根的判别式确定出m的最后取值范围．
点评：本题考查一元二次方程根与系数的关系及根的判别式．
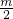，又有三角形的三边关系可得：|x1-x2|＜5，
则（x1-x2）2＜25，
即（x1+x2）2-4x1•x2＜25，
即：36-2m＜25
解得：m＞
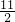；既然方程有两个实根，则△≥0，
解得m≤18．
故本题答案为：
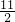＜m≤18．分析：根据一元二次方程的根与系数的关系及三角形的三边关系可得到（x1-x2）2＜25，把两根之积与两根之和代入（x1-x2）2的变形中，可求得m的取值范围，再由根的判别式确定出m的最后取值范围．
点评：本题考查一元二次方程根与系数的关系及根的判别式．
练习册系列答案
阅读快车系列答案
相关题目