题目内容
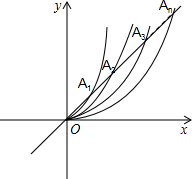 如图,直线y=x与抛物线y=ax2(a>0)在y轴右侧依次交于A1,A2,A3…An,且OA1=A1A2=A2A3=…=An-1An(n为正整数),其中经过点A1的抛物线为y=x2,则过点An的抛物线为( )
如图,直线y=x与抛物线y=ax2(a>0)在y轴右侧依次交于A1,A2,A3…An,且OA1=A1A2=A2A3=…=An-1An(n为正整数),其中经过点A1的抛物线为y=x2,则过点An的抛物线为( )分析:分别作A1B1垂直x轴,A2B2垂直x轴,…AnBn垂直x轴,先根据题意求出A1的坐标,从而利用平行线分线段成比例的知识,可求出y=x与抛物线交点坐标的特点,继而代入抛物线方程即可得出答案.
解答:解:分别作A1B1垂直x轴,A2B2垂直x轴,…AnBn垂直x轴,
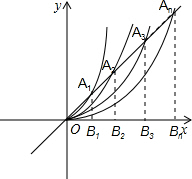
∵经过点A1的抛物线为y=x2,直线为y=x,
∴可得点A1坐标为(1,1),A1B1=1,OB1=1,
又∵A1B1∥A2B2∥AnBn,OA1=A1A2=A2A3=…=An-1An,
∴可得A1B1=1,A2B2=2,…AnBn=n,
故可得抛物线经过点(n,n),代入抛物线y=ax2(a>0),可得a=
,
故抛物线方程为:y=
x2.
故选A.

∵经过点A1的抛物线为y=x2,直线为y=x,
∴可得点A1坐标为(1,1),A1B1=1,OB1=1,
又∵A1B1∥A2B2∥AnBn,OA1=A1A2=A2A3=…=An-1An,
∴可得A1B1=1,A2B2=2,…AnBn=n,
故可得抛物线经过点(n,n),代入抛物线y=ax2(a>0),可得a=
| 1 |
| n |
故抛物线方程为:y=
| 1 |
| n |
故选A.
点评:此题属于二次函数的综合题,求出A1的坐标,利用平行线分线段成比例的知识求出An的坐标是解答本题的关键,难度一般.

练习册系列答案
相关题目
 如图,小明把小球竖直向上抛起,当小球到达最高点时球的最高点正好处于距离屋顶白炽灯10cm的位置,且灯与球心所在直线垂直于地面,这时小球在地面的影子的面积为1.92πm2.已知,灯与地面的距离为2.4m,小球的半径为
如图,小明把小球竖直向上抛起,当小球到达最高点时球的最高点正好处于距离屋顶白炽灯10cm的位置,且灯与球心所在直线垂直于地面,这时小球在地面的影子的面积为1.92πm2.已知,灯与地面的距离为2.4m,小球的半径为
 中,抛物线
中,抛物线 的解析式为
的解析式为 ,将抛物线
,将抛物线 平移后得到抛线物
平移后得到抛线物 ,若抛物线
,若抛物线 经过点(0,2),且其顶点A的横坐标为最小正整数。
经过点(0,2),且其顶点A的横坐标为最小正整数。
 (1)求这个抛物线的解析式;
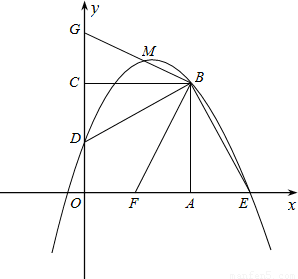
(1)求这个抛物线的解析式; ,那么结论OF=
,那么结论OF=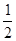 DG能成立吗?请说明理由.
DG能成立吗?请说明理由.