��Ŀ����
��ƽ��ֱ������xOy�У�����ͼ��������OABC�ı߳�Ϊ4����OA��x����������ϣ���OC��y����������ϣ���D��OC���е㣬BE��DB��x���ڵ�E.
������D��B��E�������ߵĽ���ʽ��
�ƽ���DBE�Ƶ�B��תһ���ĽǶȺ�BE���߶�OA�ڵ�F����BD��y���ڵ�G�������е���
������M�������B�غϣ��������M�ĺ�����Ϊ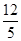 ����ô����OF=
����ô����OF=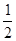 DG�ܳ�������˵������.
DG�ܳ�������˵������.
�ǹ����еĵ�F��ֱ�߽�����CB�ڵ�P�������е��������ڵ�һ���IJ����ڵ�Q����ʹ��PFEΪ���������Σ���Q�������.
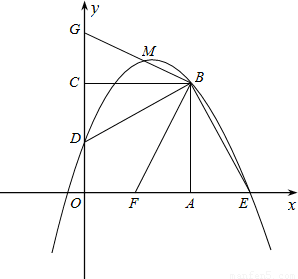
�⣺��1����BE��DB��x���ڵ�E��OABC�������Σ����DBC=EBA��
�ڡ�BCD���BAE�У��ߡ�BCD=��BAE=90�㣬 BC=BA ����DBC=��EBA ��
���BCD�ա�BAE��ASA������AE=CD��
��OABC�������Σ�OA=4��D��OC���е㣬
��A��4��0����B��4��4����C��0��4����D��0��2������E��6��0����
�����D��0��2����B��4��4����E��6��0���������߽���ʽΪy=ax2+bx+c�����У�
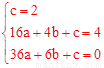 �����
����� 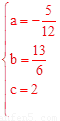 ��
��
�ྭ����D��B��E�������ߵĽ���ʽΪ��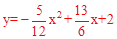 ��
��
��2������OF=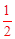 DG�ܳ������������£�
DG�ܳ������������£�
�����⣬����DBE�Ƶ�B��תһ���ĽǶȺ�ͬ����֤�á�BCG�ա�BAF����AF=CG��
��xM=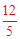 ����
����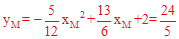 ����M��
����M��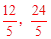 ����
����
��ֱ��MB�Ľ���ʽΪyMB=kx+b��
��M��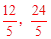 ����B��4��4����
����B��4��4����
��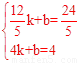 �����
�����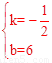 ��
��
��yMB=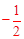 x+6����G��0��6����
x+6����G��0��6����
��CG=2��DG=4����AF=CG=2��OF=OA��AF=2��F��2��0����
��OF=2��DG=4�������OF=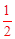 DG������
DG������
��3����ͼ����PFEΪ���������Σ���������������������������£�
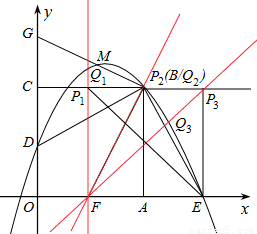
����PF=FE��
��FE=4��BC��OAƽ����֮�����Ϊ4��
���ʱP��λ������CB�ϡ�
��F��2��0������P��2��4����
��ʱֱ��FP��x�ᡣ��]��xQ=2��
��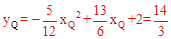 ��
��
��Q1��2��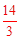 ����
����
����PF=PE��
��ͼ��ʾ����AF=AE=2��BA��FE�����BEFΪ���������Ρ�
���ʱ��P��Q���B�غϡ���Q2��4��4����
����PE=EF��
��FE=4��BC��OAƽ����֮�����Ϊ4�����ʱP��λ������CB�ϡ�
��E��6��0������P��6��4����
��ֱ��yPF�Ľ���ʽΪyPF=kx+b����F��2��0����P��6��4����
�� �����
�����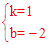 ����yPF=x��2��
����yPF=x��2��
��Q�����ֱ��PF�ϣ�Ҳ���������ϣ�
�� �������5x2��14x��48=0��
�������5x2��14x��48=0��
���x1=
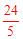 ��x2=��2���������⣬��ȥ������xQ=2��
��x2=��2���������⣬��ȥ������xQ=2��
��yQ=xQ��2=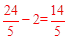 ����Q3��
����Q3��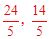 ����
����
����������Q�������ΪQ1��2��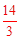 ����Q2��4��4����Q3��
����Q2��4��4����Q3��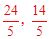 ����
����
����������1���������ε����ʺ͡�BCD�ա�BAE���E�����꣬Ȼ�����ô���ϵ�����������߽���ʽ��
��2�����M�����꣬Ȼ�����ô���ϵ������ֱ��MB�Ľ���ʽ����x=0�����G�����꣬�Ӷ��õ��߶�CG��DG�ij��ȣ��ɡ�BCG�ա�BAF���ɵ�AF=CG���Ӷ����OF�ij��ȣ��Ƚ�OF��DG�ij��ȣ���������OF=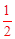 DG�Ĺ�ϵ�����Խ��۳�����
DG�Ĺ�ϵ�����Խ��۳�����
��3����PF=FE��PF=PE��PE=EF�����������һ���۲���⡣

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д� ��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ�����
��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ����� ��2013•˳������ģ����ͼ����ƽ��ֱ������xOyϵ��һ�κ���y=-2x+2��ͼ����x���ཻ�ڵ�B����y���ཻ�ڵ�C���뷴��������ͼ���ཻ�ڵ�A����AB=2BC��
��2013•˳������ģ����ͼ����ƽ��ֱ������xOyϵ��һ�κ���y=-2x+2��ͼ����x���ཻ�ڵ�B����y���ཻ�ڵ�C���뷴��������ͼ���ཻ�ڵ�A����AB=2BC�� ��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������
��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������