Question

【题目】如图1，在正方形和正方形中，边在边上，正方形绕点按逆时针方向旋转

（1）如图2，当时，求证：；

（2）在旋转的过程中，设的延长线交直线于点．①如果存在某一时刻使得，请求出此时的长；②若正方形绕点按逆时针方向旋转了，求旋转过程中，点运动的路径长．

Answer 1

【答案】（1）见详解;(2) ;.

【解析】

（1）由正方形的性质得出AD＝AB，AG＝AE，∠BAD＝∠EAG＝90°，由∠BAE＋∠EAD＝∠BAD，∠DAG＋∠EAD＝∠EAG，推出∠BAE＝∠DAG，由SAS即可证得△DAG≌△BAE；

（2）①由AB＝2，AE＝1，由勾股定理得AF＝AE＝，易证△ABF是等腰三角形，由AE＝EF，则直线BE是AF的垂直平分线，设BE的延长线交AF于点O，交AD于点H，则OE＝OA＝，由勾股定理得OB=，由cos∠ABO＝，cos∠ABH＝，求得BH＝，由勾股定理得AH＝=，则DH＝ADAH＝2，由∠DHP＝∠BHA，∠BAH＝∠DPH＝90°，证得△BAH∽△DPH，得出，即可求得DP；

②由△DAG≌△BAE，得出∠ABE＝∠ADG，由∠BPD＝∠BAD＝90°，则点P的运动轨迹为以BD为直径的，由正方形的性质得出BD＝AB＝2，由正方形AEFG绕点A按逆时针方向旋转了60°，得出∠BAE＝60°，由AB＝2AE，得出∠BEA＝90°，∠ABE＝30°，B、E、F三点共线，同理D、F、G三点共线，则P与F重合，得出∠ABP＝30°，则所对的圆心角为60°，由弧长公式即可得出结果．

解答：（1）证明：在正方形ABCD和正方形AEFG中，AD＝AB，AGspan>＝AE，∠BAD＝∠EAG＝90°，

∵∠BAE＋∠EAD＝∠BAD，∠DAG＋∠EAD＝∠EAG，

∴∠BAE＝∠DAG，

在△DAG和△BAE中，

，

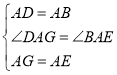∴△DAG≌△BAE（SAS）；

∴BE＝DG；

（2）解：①∵AB＝2AE＝2，

∴AE＝1，

由勾股定理得，AF＝AE＝，

∵BF＝BC＝2，

∴AB＝BF＝2，

∴△ABF是等腰三角形，

∵AE＝EF，

∴直线BE是AF的垂直平分线

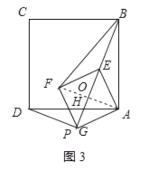
，设BE的延长线交AF于点O，交AD于点H，如图3所示：

则OE＝OA＝，

∴OB=，

∵cos∠ABO＝，cos∠ABH＝，

∴BH＝，

AH＝=，

∴DH＝ADAH＝2，

∵∠DHP＝∠BHA，∠BAH＝∠DPH＝90°，

∴△BAH∽△DPH，

∴，

即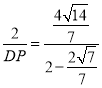

∴DP＝；

②

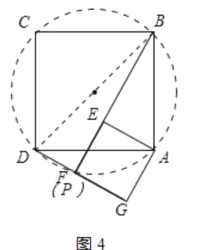
∵△DAG≌△BAE，

∴∠ABE＝∠ADG，

∵∠BPD＝∠BAD＝90°，

∴点P的运动轨迹为以BD为直径的，

BD＝AB＝2，

∵正方形AEFG绕点A按逆时针方向旋转了60°，

∴∠BAE＝60°，

∵AB＝2AE，

∴∠BEA＝90°，∠ABE＝30°，

∴B、E、F三点共线，

同理D、F、G三点共线，

∴P与F重合，

∴∠ABP＝30°，

∴所对的圆心角为60°，

∴旋转过程中点P运动的路线长为：.