题目内容
【题目】如图所示,等腰![]() 的周长为
的周长为![]() ,底边为
,底边为![]() ,
, ![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(![]() )求
)求![]() 的周长;
的周长;
(![]() )若
)若![]() ,
, ![]() 为
为![]() 上一点,连结
上一点,连结![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.

【答案】(1)13;(2)![]() .
.
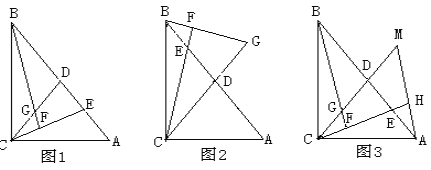
【解析】试题分析:(1)根据线段垂直平分线的定义得出AE=BE,则△BEC的周长转化为AE+EC+BC,即求AC+BC,则求出AC即可;(2)作点D关于AC的对称点F,连接AF,FP,BF,此时PD=PF,则DP+BP最小即为PF+BP最小,则当P、B、F共线时DP+BP最小,最小为线段BF的长,此时可求出∠BAF=60°,∠ABF=30°,则可得∠AFB=90°,根据勾股定理求解.
解:(1)∵等腰△ABC周长21,底边BC=5,
∴腰长AB=AC=(21-5)÷2=8,
∵DE为AB的垂直平分线,
∴AE=BE,
∴△BEC的周长为BE+EC+BC=AE+EC+BC=AC+BC=13.
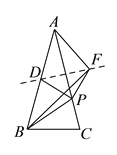
(2)作点D关于AC的对称点F,连接AF,FP,BF,
则当P、B、F共线时DP+BP最小,最小为线段BF的长,
∵∠BAC=∠CAF=30°,
∴∠DAF=60°,且DA=DB=AF=4,
∴△ADF为等边三角形,
∴∠ADF=60°,DF=DB=4,
∴∠DBF=∠DFB=30°,
∴∠AFB=∠AFD+∠DFB=90°,
∴△ABF为直角三角形,,
∴BF=![]() =4
=4![]() ,
,
∴PD+BP最小值为![]() .
.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目