题目内容
【题目】有4张正面分别标有数字
的不透明卡片，它们除数字不同外其余全部相同，现将它们背面朝上，洗匀后从中任取一张，将卡片上的数字记为
，另有一个被均匀分成4份的转盘，上面分别标有数字
，转动转盘，指针所指的数字记为
（若指针指在分割线上则重新转一次），则点
落在抛物线
与
轴所围成的区域内（不含边界）的概率是__________．
【答案】
【解析】利用列表法作出所有等可能的情况，然后据二次函数图象上点的坐标特征求出落在抛物线与x轴围成的区域内的点的个数，再根据概率公式列式计算即可得解．
解：列表如下：
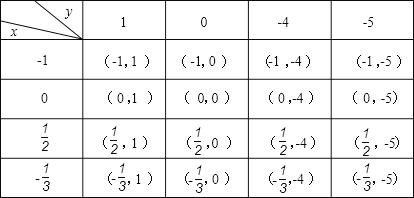
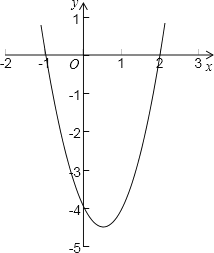
当x=-1时，y=2x2-2x-4=2×（-1）2-2×（-1）-4=2+2-4=0，
所以，没有点落在抛物线与x轴围成的区域内，
当x=0时，y=-4，
所以，没有点落在抛物线与x轴围成的区域内，
当x=
时，y=2x2-2x-4=2×（
）2-2×-4=-1-4=-4，
所以，点（，-4）落在抛物线与x轴围成的区域内，当x=-
时，y=2x2-2x-4=2×（-
）2-2×（-）-4=
+
-4=-3
，
所以，没有点落在抛物线与x轴围成的区域内，
综上所述，点P一共有16种情况，落在抛物线与x轴围成的区域内的点只有（
，-4）一个，
所以P（落在抛物线与x轴围成的区域内）=．
故答案为：．
本题考查了列表法以及概率公式，用到的知识点为：概率=所求情况数与总情况数之比．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】包河区发展农业经济产业，在大圩乡种植多品种的葡萄.已知某葡萄种植户李大爷的葡萄成本为10元
，如果在未来40天葡萄的销售单价
（元）与时间
（天）之间的函数关系式为：
，且葡萄的日销售量
（千克）与时间（天）的关系如下表：
时间 | 1 | 3 | 6 | 10 | 20 | 40 |
日销售量 | 118 | 114 | 108 | 100 | 80 | 40 |
（1）请直接写出与之间的变化规律符合什么函数关系？并求在第15天的日销售量是多少千克？
（2）在后20天（即
），请求出哪一天的日销售利润最大？日销售利润最大为多少？
（3）在实际销售的前20天中，李大爷决定每销售1千克水果就捐赠
元利润（
）给留守贫困儿童作为助学金，前20天销售完后李大爷发现，每天扣除捐赠后的日销售利润随时间
的增大而增大，请求出的取值范围.
