��Ŀ����
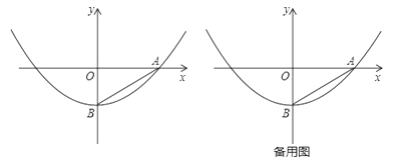
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�Rt��AOB��ֱ�DZ�OA��x���������ϣ�OB��y�Ḻ�����ϣ���OA=![]() ��OB=1���Ե�BΪ����������߾�����A��
��OB=1���Ե�BΪ����������߾�����A��
��1������������ߵĽ���ʽ��
��2���ڶ������ڵĵ�M���Ǿ���ԭ����ƽ��Rt��AOB�����ֱ����һ�㣮��OM=2�����жϵ�M�Ƿ��ڣ�1���е��������ϣ���˵�����ɣ�
��3����P�Ǿ�����B���������ƽ�е�ֱ��l��һ�㣮����̽������ֱ��l�Ƶ�B������ת������������ƽ�л��غϣ�ʱ���Ƿ����������ֱ��l����ֱ��l�����ҵ���P��ʹ��PAB��Rt��AOB���ƣ����ƱȲ�Ϊ1���������ڣ����ֱ��l�Ľ���ʽ���������ڣ�˵�����ɣ�
���𰸡���1��y=![]() x2��1��2����M����������y=
x2��1��2����M����������y=![]() x2��1�ϣ�3����������ֱ��l��y=��
x2��1�ϣ�3����������ֱ��l��y=��![]() x��1��y=��
x��1��y=��![]() x��1��y=
x��1��y=![]() x��1��������ֱ��l�����ҵ���P��ʹRt��PAB��Rt��AOB����
x��1��������ֱ��l�����ҵ���P��ʹRt��PAB��Rt��AOB����
��������
��1��������õ�A��B�����꣬����BΪ�����ߵĶ��㣬��������ߵĽ���ʽ����A����������a��ֵ������ȷ���������߽���ʽ��
��2����M�����������ϣ�����Ϊ������������x�����һ������ΪC��ֱ��OM��AB�ڵ�D��������õ�DΪAB���е㣬�õ�AD=OD=BD���õ���MON=��AOD=��OAD=30������MN��ֱ��OC�����MN��ON�ij���ȷ����M���꣬���������߽���ʽ���鼴�ɵõ������
��3�����ڣ���Rt��AOB�У�AO=![]() ��BO=1��AB=2����ABO=60�㣬��BAO=30����������������ǣ�������ABP=90��ʱ������AP1B=60��������ABP1�ס�AOB�������Ƶñ�����ȷ����P1�����꣬����B����ȷ����ֱ��l����ʽ���ɣ�������ABP=60��ʱ������BAP5=90��������ABP5�ס�OBA�������Ƶñ������P5���꣬ͬ��ȷ����ֱ��l����ʽ��������ABP=30����ֱ��l��AB�Ϸ�ʱ������P6AB=90��������ABP6�ס�OAB�������Ƶñ������P6���꣬ͬ��ȷ����ֱ��l����ʽ�����ϣ��õ�ֱ��l�����ҵ���P��ʹRt��PAB��Rt��AOB����ʱ�����н���ʽ��
��BO=1��AB=2����ABO=60�㣬��BAO=30����������������ǣ�������ABP=90��ʱ������AP1B=60��������ABP1�ס�AOB�������Ƶñ�����ȷ����P1�����꣬����B����ȷ����ֱ��l����ʽ���ɣ�������ABP=60��ʱ������BAP5=90��������ABP5�ס�OBA�������Ƶñ������P5���꣬ͬ��ȷ����ֱ��l����ʽ��������ABP=30����ֱ��l��AB�Ϸ�ʱ������P6AB=90��������ABP6�ס�OAB�������Ƶñ������P6���꣬ͬ��ȷ����ֱ��l����ʽ�����ϣ��õ�ֱ��l�����ҵ���P��ʹRt��PAB��Rt��AOB����ʱ�����н���ʽ��
��1��������ã�A��![]() ��0����B��0����1����
��0����B��0����1����
��BΪ�����ߵĶ��㣬
���������߽���ʽΪy=ax2��1��
��A�������ã�3a��1=0����a=![]() ��
��
�������߽���ʽΪy=![]() x2��1��
x2��1��
��2����M����������y=![]() x2��1�ϣ�����Ϊ��
x2��1�ϣ�����Ϊ��
����������x�����һ������ΪC��ֱ��OM��AB�ڵ�D����MN��OC�ڵ�N��
������ã�DΪAB���е㣬��OD=AD=BD��
���MON=��AOD=��OAD=30�㣬
��Rt��OMN��OM=2��
��MN=1��ON=![]() ����M����
����M����![]() ��1����
��1����
��y=![]() ������
������![]() ��2��1=0��1��
��2��1=0��1��
���M����������y=![]() x2��1�ϣ�
x2��1�ϣ�
��3�����ڣ���Rt��AOB�У�AO=![]() ��BO=1��AB=2����ABO=60�㣬��BAO=30�㣬
��BO=1��AB=2����ABO=60�㣬��BAO=30�㣬
������������ǣ�
�ٵ���ABP=90��ʱ������AP1B=60�㣬���ABP1�ס�AOB��
��![]() =
=![]() ����BP1=
����BP1=![]() =
=![]() ��
��
��OP1=![]() ����P1����
����P1����![]() ��0����[����Ҳ�������P2����
��0����[����Ҳ�������P2����![]() ��2����P3��
��2����P3��![]() ����2����P4��
����2����P4��![]() ����4��]��
����4��]��
��ֱ��l����ʽΪy=kx+b����B��P1�������ã�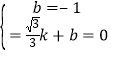 ��
��
��ã�![]() ��
��
��ʱֱ��l����ʽΪy=��![]() x��1��
x��1��
�ڵ���ABP=60��ʱ������BAP5=90�㣬���ABP5�ס�OBA��
��![]() =
=![]() ����BP5=
����BP5=![]() =4��
=4��
��P5��P5C��y���ڵ�G����Rt��BGP5�У���P5BG=60�㣬
��P5G=2![]() ��BG=2����P5��2
��BG=2����P5��2![]() ����3����
����3����
ͬ�����ֱ��l����ʽΪy=��![]() x��1��
x��1��
�۵���ABP=30����ֱ��l��AB�Ϸ�ʱ������P6AB=90�㣬���ABP6�ס�OAB��
��![]() =
=![]() ����BP6=
����BP6=![]() =
=![]() ��
��
��P6��P6H��y���ڵ�H����Rt��BP6H�У���P6BH=30�㣬
��P6H=![]() ��BH=2��
��BH=2��
��P6��![]() ��1����
��1����
ͬ���õ�ֱ��l����ʽΪy=![]() x��1��
x��1��
���ϣ���������ֱ��l��y=��![]() x��1��y=��
x��1��y=��![]() x��1��y=
x��1��y=![]() x��1��������ֱ��l�����ҵ���P��ʹRt��PAB��Rt��AOB���ƣ�
x��1��������ֱ��l�����ҵ���P��ʹRt��PAB��Rt��AOB���ƣ�

 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�