Question

解答下列各题：
（1）如图，写出△ABC的各顶点坐标，并画出△ABC关于y轴对称的△A₁B₁C₁，写出△ABC关于x轴对称的△A₂B₂C₂的各点坐标．
（2）若|3a-2|+|b-3|=0，求P（-a，b）关于y轴的对轴点P′的坐标．

Answer 1

分析：（1）根据平面直角坐标系写出点A、B、C的坐标即可；再根据网格结构找出点A、B、C的对应点的位置，然后顺次连接即可；
（2）根据非负数的性质列式求出a、b的值，从而得到点P的坐标，再根据关于y轴对称的点的横坐标互为相反数，纵坐标相等解答．

解答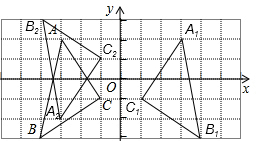：解：（1）A（-3，2），B（-4，-3），C（-1，-1）；
△A₁B₁C₁与△A₂B₂C₂如图所示；
A₂（-3，-2），B₂（-4，3），C₂（-1，1）；

（2）根据题意得，3a-2=0，b-3=0，
解得a=

2

3

，b=3，
所以点P的坐标为（-

2

3

，3），
∵P（-a，b）关于y轴的对轴点为P′，
∴P（

2

3

，3）．

点评：本题考查了利用轴对称变换作图，绝对值非负数的性质，关于y轴对称的点的坐标的横坐标互为相反数，纵坐标相同，熟练掌握网格结构是解题的关键．