题目内容
【题目】如图,点D是∠AOB内一点,点E,F分别在OA,OB上,且OE<OF,DE=DF,∠OED+∠OFD=180°,

(1)请作出点D到OA,OB的距离,标明垂足;
(2)求证:OD平分∠AOB;
(3)若∠AOB=60°,OD=6,OE=4,求△ODE的面积。
【答案】(1)见解析;(2)见解析;(3)6
【解析】
(1)利用垂直的画法可分别作DM⊥OA,DN⊥OB,则DM、DN分别为点D到OA、OB的距离;
(2)根据(1)中作图,结合条件可证明△EDM≌△FDN,可证得DM=DN,由角平分线的判定可证得OD平分∠AOB.
(3)根据角平分线的性质得到∠DOE=![]() ,因为DM⊥OA,所以
,因为DM⊥OA,所以![]() ,再根据三角形面积公式进行计算即可得到答案.
,再根据三角形面积公式进行计算即可得到答案.
(1)如图,过点D作DM⊥OA于M,DN⊥OB于N,则DM,DN分别为点D到OA,OB的距离;
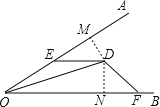
(2)证明:∵DM⊥OA,DN⊥OB
∴∠DME=∠DNF=90°.
∵∠OED+∠OFD=180°,且∠OED+∠MED=180°,
∴∠MED=∠OFD.
又∵DE=DF,
∴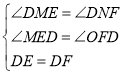
∴△EDM≌△FDN(AAS),
∴DM=DN.
∵DM⊥OA,DN⊥OB,
∴OD平分∠AOB.
(3)∵OD平分∠AOB,
∴∠DOE=![]() ,
,
∵DM⊥OA,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目